UMAC

This article is about a cryptographic authentication code. For the athletic organization, see Upper Midwest Athletic Conference.

In cryptography, a message authentication code based on universal hashing, or UMAC, is a type of message authentication code (MAC) calculated choosing a hash function from a class of hash functions according to some secret (random) process and applying it to the message. The resulting digest or fingerprint is then encrypted to hide the identity of the hash function used. As with any MAC, it may be used to simultaneously verify both the data integrity and the authenticity of a message. UMAC is specified in RFC 4418, it has provable cryptographic strength and is usually a lot less computationally intensive than other MACs. UMAC's design is optimized for 32-bit architectures; a closely related variant of UMAC that is optimized for 64-bit architectures is given by VMAC.

Universal hashing

Main article: universal hashing

Let's say the hash function is chosen from a class of hash functions H, which maps messages into D, the set of possible message digests. This class is called universal if, for any distinct pair of messages, there are at most |H|/|D| functions that map them to the same member of D.

This means that if an attacker wants to replace one message with another and, from his point of view the hash function was chosen completely randomly, the probability that the UMAC will not detect his modification is at most 1/|D|.

But this definition is not strong enough — if the possible messages are 0 and 1, D={0,1} and H consists of the identity operation and not, H is universal. But even if the digest is encrypted by modular addition, the attacker can change the message and the digest at the same time and the receiver wouldn't know the difference.

Strongly universal hashing

A class of hash functions H that is good to use will make it difficult for an attacker to guess the correct digest d of a fake message f after intercepting one message a with digest c. In other words

\Pr_{h \in H}[h(f)=d|h(a)=c]\,

needs to be very small, preferably 1/|D|.

It is easy to construct a class of hash functions when D is field. For example if |D| is prime, all the operations are taken modulo |D|. The message a is then encoded as an n-dimensional vector over D (a₁, a₂, ..., a_n). H then has |D|ⁿ⁺¹ members, each corresponding to an (n + 1)-dimensional vector over D (h₀, h₁, ..., h_n). If we let

h(a)=h_0+\sum_{i=1}^n h_ia_i\,

we can use the rules of probabilities and combinatorics to prove that

\Pr_{h \in H}[h(f)=d|h(a)=c]={1 \over |D|}

If we properly encrypt all the digests (e.g. with a one-time pad), an attacker cannot learn anything from them and the same hash function can be used for all communication between the two parties. This may not be true for ECB encryption because it may be quite likely that two messages produce the same hash value. Then some kind of initialization vector should be used, which is often called the nonce. It has become common practice to set h₀ = f(nonce), where f is also secret.

Notice that having massive amounts of computer power does not help the attacker at all. If the recipient limits the amount of forgeries it accepts (by sleeping whenever it detects one), |D| can be 2³² or smaller.

NH hash-function family

Functions in the above unnamed hash-function family uses n multiplies to compute a hash value.

UMAC is the first MAC specifically designed to use SIMD instructions.^[1]

For speed, UMAC uses the NH hash-function family. The NH family halves the number of multiplications, which roughly translates to a two-fold speed-up in practice.^[2]

The following hash family is universal:^[1]

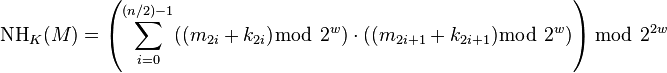\operatorname{NH}_{K}(M) = \left( \sum_{i=0}^{ (n/2)-1 } ((m_{2i} + k_{2i}) \bmod ~ 2^w ) \cdot ((m_{2i+1} + k_{2i+1}) \bmod ~ 2^w ) \right) \bmod ~ 2^{2w}

where

The message M is encoded as an n-dimensional vector of w-bit words (m₀, m₁, m₂, ..., m_n-1).
The intermediate key K is encoded as an n+1-dimensional vector of w-bit words (k₀, k₁, k₂, ..., k_n). A pseudorandom generator generates K from a shared secret key.

If double-precision operations are not available, one can interpret the input as a vector of half-words (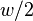 $w/2$ -bit integers). The algorithm will then use 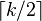$\lceil k/2 \rceil$ multiplications, where $k$ was the number of half-words in the vector. Thus, the algorithm runs at a "rate" of one multiplication per word of input.

Example

The following C function generates a 24 bit UMAC. It assumes that secret is a multiple of 24 bits, msg is not longer than secret and result already contains the 24 secret bits e.g. f(nonce). nonce does not need to be contained in msg.

  #define uchar unsigned char
  
  void UHash24 (uchar *msg, uchar *secret, int len, uchar *result)
  {
    uchar r1 = 0, r2 = 0, r3 = 0, s1, s2, s3, byteCnt = 0, bitCnt, byte;
     
    while (len-- > 0) {    
      if (byteCnt-- == 0) {
        s1 = *secret++;
        s2 = *secret++;
        s3 = *secret++;
        byteCnt = 2;   
      }             
      byte = *msg++;
      for (bitCnt = 0; bitCnt < 8; bitCnt++) {
        if (byte & 1) { /* msg not divisible by x */
          r1 ^= s1; /* so add s * 1 */                                 
          r2 ^= s2;
          r3 ^= s3;        
        }
        byte >>= 1; /* divide message by x */
        if (s3 & 0x80) { /* and multiply secret with x, subtracting
            the polynomial when necessary to keep its order under 24 */
          s3 <<= 1;
          if (s2 & 0x80) s3 |= 1;
          s2 <<= 1;
          if (s1 & 0x80) s2 |= 1;
          s1 <<= 1;
        
          s1 ^= 0x1B; /* x^24 + x^4 + x^3 + x + 1 */
        }
        else {
          s3 <<= 1;
          if (s2 & 0x80) s3 |= 1;
          s2 <<= 1;
          if (s1 & 0x80) s2 |= 1;
          s1 <<= 1;
        }
      } /* for each bit in the message */
    } /* for each byte in the message */ 
    *result++ ^= r1;
    *result++ ^= r2;
    *result++ ^= r3;
  }

References

1 2 Black, J.; Halevi, S.; Krawczyk, H.; Krovetz, T. (1999). UMAC: Fast and Secure Message Authentication (PDF). Advances in Cryptology (CRYPTO '99). , Equation 1 and also section 4.2 "Definition of NH".
↑ Thorup, Mikkel (2009). String hashing for linear probing. Proc. 20th ACM-SIAM Symposium on Discrete Algorithms (SODA). pp. 655–664. doi:10.1137/1.9781611973068.72. Archived (PDF) from the original on 2013-10-12. , section 5.3

UMAC has been approved by the IETF as an informational RFC. It's fast and based on AES.
A draft specification to use UMAC in the SSH protocols has been implemented by OpenSSH.

Hash functions & message authentication codes

Security summary

Common functions	MD5 SHA-1 SHA-2 SHA-3/Keccak

SHA-3 finalists	BLAKE Grøstl JH Skein Keccak (winner)

Other functions	FSB ECOH GOST HAS-160 HAVAL Kupyna LM hash MDC-2 MD2 MD4 MD5 MD6 N-Hash RadioGatún RIPEMD SipHash Snefru Streebog SWIFFT Tiger VSH WHIRLPOOL

MAC algorithms	DAA CBC-MAC HMAC OMAC/CMAC PMAC VMAC UMAC Poly1305

Authenticated encryption modes	CCM CWC EAX GCM IAPM OCB

Attacks	Collision attack Preimage attack Birthday attack Brute force attack Rainbow table Side-channel attack Length extension attack

Design	Avalanche effect Hash collision Merkle–Damgård construction

Standardization	CRYPTREC NESSIE NIST hash function competition

Utilization	Salt Key stretching Message authentication

Key derivation functions	bcrypt crypt(3) (DES) PBKDF2 scrypt Argon2

Cryptography

History of cryptography Cryptanalysis Outline of cryptography

Symmetric-key algorithm Block cipher Stream cipher Public-key cryptography Cryptographic hash function Message authentication code Random numbers Steganography

Portal

This article is issued from Wikipedia - version of the Sunday, June 14, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.