Tutte theorem

Not to be confused with Tutte homotopy theorem or Tutte's spring theorem.

In the mathematical discipline of graph theory the Tutte theorem, named after William Thomas Tutte, is a characterization of graphs with perfect matchings. It is a generalization of Hall's marriage theorem from bipartite to arbitrary graphs and is a special case of the Tutte–Berge formula.

Tutte's theorem

A graph, G = (V, E), has a perfect matching if and only if for every subset U of V, the subgraph induced by V − U has at most |U| connected components with an odd number of vertices.[1]

Proof

First we write the condition:

(*) \qquad \forall U \subseteq V, \quad o(G-U)\le|U|

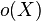where o(X) denotes the number of odd components of the subgraph induced by X.

Necessity of (∗): Consider a graph G, with a perfect matching. Let U be an arbitrary subset of V. Delete U. Let C be an arbitrary odd component in G − U. Since G had a perfect matching, at least one vertex in C must be matched to a vertex in U. Hence, each odd component has at least one vertex matched with a vertex in U. Since each vertex in U can be in this relation with at most one connected component (because of it being matched at most once in a perfect matching), o(G − U) ≤ |U|.[2]

Sufficiency of (∗): Let G be an arbitrary graph with no perfect matching. We will find a bad set of vertices S, that is, a subset of V such that |S| < o(G − S). We can suppose that G is edge-maximal, i.e., G + e has a perfect matching for every edge e not present in G already. Indeed, if we find a bad set S in edge-maximal graph G, then S is also a bad set in every spanning subgraph of G, as every odd component of G − S will be split into possibly more components at least one of which will again be odd.

We define S to be the set of vertices with degree |V| − 1. First we consider the case where all components of G − S are complete graphs. Then S has to be a bad set, since if o(G − S) ≤ |S|, then we could find a perfect matching by matching one vertex from every odd component with a vertex from S and pairing up all other vertices (this will work unless |V| is odd, but then ∅ is bad).

Now suppose that K is a component of G − S and x, y ∈ K are vertices such that xy ∉ E. Let x, a, b ∈ K be the first vertices on a shortest x,y-path in K. This ensures that xa, ab ∈ E and xb ∉ E. Since a ∉ S, there exists a vertex c such that ac ∉ E. From the edge-maximality of G, we define M1 as a perfect matching in G + xb and M2 as a perfect matching in G + ac. Observe that surely xb ∈ M1 and ac ∈ M2.

Let P be the maximal path in G that starts from c with an edge from M1 and whose edges alternate between M1 and M2. How can P end? Unless we are arrive at 'special' vertex such as x, a or b, we can always continue: c is M2-matched by ca, so the first edge of P is not in M2, therefore the second vertex is M2-matched by a different vertex and we continue in this manner.

Let v denote the last vertex of P. If the last edge of P is in M1, then v has to be a, since otherwise we could continue with an edge from M2 (even to arrive at x or b). In this case we define C:=P + ac. If the last edge of P is in M2, then surely v ∈ {x, b} for analoguous reason and we define C:=P + va + ac.

Now C is a cycle in G + ac of even length with every other edge in M2. We can now define M:=M2 Δ C (where Δ is symmetric difference) and we obtain a matching in G, a contradiction.

See also

Notes

  1. ↑ Lovász & Plummer (1986), p.  84; Bondy & Murty (1976), Theorem 5.4, p. 76.
  2. ↑ Bondy & Murty (1976), pp. 76–78.

References

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.