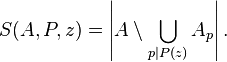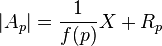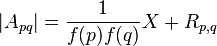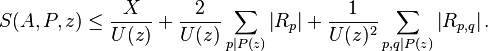Turán sieve

In number theory, the Turán sieve is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences. It was developed by Pál Turán in 1934.

Description

In terms of sieve theory the Turán sieve is of combinatorial type: deriving from a rudimentary form of the inclusion-exclusion principle. The result gives an upper bound for the size of the sifted set.

Let A be a set of positive integers ≤ x and let P be a set of primes. For each p in P, let A_p denote the set of elements of A divisible by p and extend this to let A_d be the intersection of the A_p for p dividing d, when d is a product of distinct primes from P. Further let A₁ denote A itself. Let z be a positive real number and P(z) denote the product of the primes in P which are ≤ z. The object of the sieve is to estimate

S(A,P,z) = \left\vert A \setminus \bigcup_{p \mid P(z)} A_p \right\vert .

We assume that |A_d| may be estimated, when d is a prime p by

\left\vert A_p \right\vert = \frac{1}{f(p)} X + R_p

and when d is a product of two distinct primes d = p q by

\left\vert A_{pq} \right\vert = \frac{1}{f(p)f(q)} X + R_{p,q}

where X = |A| and f is a function with the property that 0 ≤ f(d) ≤ 1. Put

U(z) = \sum_{p \mid P(z)} f(p) .

Then

S(A,P,z) \le \frac{X}{U(z)} + \frac{2}{U(z)} \sum_{p \mid P(z)} \left\vert R_p \right\vert + \frac{1}{U(z)^2} \sum_{p,q \mid P(z)} \left\vert R_{p,q} \right\vert .

Applications

The Hardy–Ramanujan theorem that the normal order of ω(n), the number of distinct prime factors of a number n, is log(log(n));
Almost all integer polynomials (taken in order of height) are irreducible.

References

Alina Carmen Cojocaru; M. Ram Murty. An introduction to sieve methods and their applications. London Mathematical Society Student Texts 66. Cambridge University Press. pp. 47–62. ISBN 0-521-61275-6.
Greaves, George (2001). Sieves in number theory. Springer-Verlag. ISBN 3-540-41647-1.
Halberstam, Heini; Richert, H.-E. (1974). Sieve Methods. London Mathematical Society Monographs 4. Academic Press. ISBN 0-12-318250-6. MR 54:12689. Zbl 0298.10026.
Christopher Hooley (1976). Applications of sieve methods to the theory of numbers. Cambridge University Press. p. 21. ISBN 0-521-20915-3.

This article is issued from Wikipedia - version of the Thursday, September 10, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.