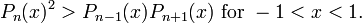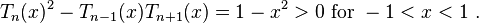Turán's inequalities

In mathematics, Turán's inequalities are some inequalities for Legendre polynomials found by Paul Turán (1950) (and first published by Szegö (1948)). There are many generalizations to other polynomials, often called Turán's inequalities, given by (E. F. Beckenbach, W. Seidel & Otto Szász 1951) and other authors.

If $P n$ is the $n$ th Legendre polynomial, Turán's inequalities state that

\,\! P_n(x)^2 > P_{n-1}(x)P_{n+1}(x)\text{ for }-1<x<1.

For H_n, the nth Hermite polynomial, Turán's inequalities are

H_n(x)^2 - H_{n-1}(x)H_{n+1}(x)= (n-1)!\cdot \sum_{i=0}^{n-1}\frac{2^{n-i}}{i!}H_i(x)^2>0 ~,

whilst for Chebyshev polynomials they are

\! T_n(x)^2 - T_{n-1}(x)T_{n+1}(x)= 1-x^2>0 \text{ for }-1<x<1~.

References

Beckenbach, E. F.; Seidel, W.; Szász, Otto (1951), "Recurrent determinants of Legendre and of ultraspherical polynomials", Duke Math. J. 18: 1–10, doi:10.1215/S0012-7094-51-01801-7, MR 0040487
Szegö, G. (1948), "On an inequality of P. Turán concerning Legendre polynomials", Bull. Amer. Math. Soc. 54 (4): 401–405, doi:10.1090/S0002-9904-1948-09017-6, MR 0023954
Turán, Paul (1950), "On the zeros of the polynomials of Legendre", Časopis Pěst. Mat. Fys. 75: 113–122, MR 0041284

This article is issued from Wikipedia - version of the Thursday, December 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Turán's inequalities

See also

References