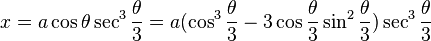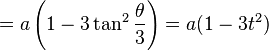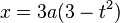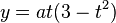Tschirnhausen cubic

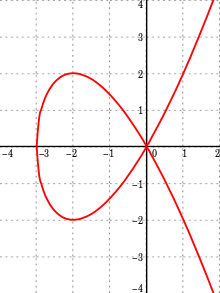
The Tschirnhausen cubic,

y^2=x^3+3x^2.

In geometry, the Tschirnhausen cubic, or Tschirnhaus' cubic is a plane curve defined by the polar equation

r = a\sec^3(\theta/3).

History

The curve was studied by von Tschirnhaus, de L'Hôpital, and Catalan. It was given the name Tschirnhausen cubic in a 1900 paper by R C Archibald, though it is sometimes known as de L'Hôpital's cubic or the trisectrix of Catalan.

Other equations

Put 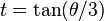$t=\tan(\theta/3)$ . Then applying triple-angle formulas gives

x=a\cos \theta \sec^3 \frac{\theta}{3} = a(\cos^3 \frac{\theta}{3} - 3 \cos \frac{\theta}{3} \sin^2 \frac{\theta}{3}) \sec^3 \frac{\theta}{3}

= a\left(1 - 3 \tan^2 \frac{\theta}{3}\right)= a(1 - 3t^2)

y=a\sin \theta \sec^3 \frac{\theta}{3} = a \left(3 \cos^2 \frac{\theta}{3}\sin \frac{\theta}{3} - \sin^3 \frac{\theta}{3} \right) \sec^3 \frac{\theta}{3}

= a \left(3 \tan \frac{\theta}{3} - \tan^3 \frac{\theta}{3} \right) = at(3-t^2)

giving a parametric form for the curve. The parameter t can be eliminated easily giving the Cartesian equation

27ay^2 = (a-x)(8a+x)^2

If the curve is translated horizontally by 8a then the equations become

x = 3a(3-t^2)

y = at(3-t^2)

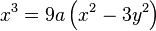x^3=9a \left(x^2-3y^2 \right)

This gives an alternate polar form of

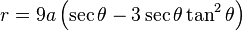r=9a \left(\sec \theta - 3\sec \theta \tan^2 \theta \right)

References

J. D. Lawrence, A Catalog of Special Plane Curves. New York: Dover, 1972, pp. 87-90.

External links

This article is issued from Wikipedia - version of the Monday, December 01, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.