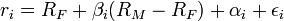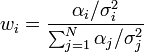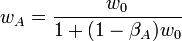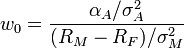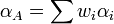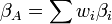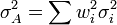Treynor–Black model

In Finance the Treynor–Black model is a mathematical model for security selection published by Fischer Black and Jack Treynor in 1973. The model assumes an investor who considers that most securities are priced efficiently, but who believes he has information that can be used to predict the abnormal performance (Alpha) of a few of them; the model finds the optimum portfolio to hold under such conditions.

In essence the optimal portfolio consists of two parts: a passively invested index fund containing all securities in proportion to their market value and an 'active portfolio' containing the securities for which the investor has made a prediction about alpha. In the active portfolio the weight of each stock is proportional to the alpha value divided by the variance of the residual risk.

The Model

Assume that the risk free rate is R_F and the expected market return is R_M with standard deviation 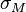$\sigma_M$ . There are N securities that have been analyzed and are thought to be mispriced, with expected returns given by:

r_i = R_F +\beta_i(R_M-R_F)+\alpha_i+\epsilon_i

where the random terms $\epsilon_i$ are normally distributed with mean 0, standard deviation $\sigma_i$ , and are mutually uncorrelated. (This is the so-called Diagonal Model of Stock Returns, or Single-index model due to William F. Sharpe).

Then^[1] it was shown by Treynor and Black that the active portfolio A is constructed using the weights

w_i = \frac{\alpha_i/\sigma_i^2}{\sum_{j=1}^N \alpha_j/\sigma_j^2}

(Note that if an alpha is negative the corresponding portfolio weight will also be negative, i.e. the active portfolio is in general a long-short portfolio).

The overall risky portfolio for the investor consists of a fraction w_A invested in the active portfolio and the remainder (i.e. 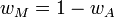$w_M=1-w_A$ ) invested in the market portfolio. This fraction is found as follows:

w_A = \frac{w_0}{1+(1-\beta_A)w_0}

w_0 = \frac{\alpha_A/\sigma_A^2}{(R_M-R_F)/\sigma_M^2}

where the alpha, beta and residual risk of A are found using the previously computed weights w_i in the obvious way

\alpha_A=\sum w_i \alpha_i

\beta_A=\sum w_i \beta_i

\sigma_A^2=\sum w_i^2 \sigma_i^2

References

↑ Kane et al.

Treynor, J. L. and F. Black, 1973, How to Use Security Analysis to Improve Portfolio Selection, Journal of Business, January, pages 66–88. JSTOR 2351280
Kane, Kim and White: Active Portfolio Management - The power of the Treynor–Black model, December 2003,

This article is issued from Wikipedia - version of the Thursday, March 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.