Transmission-line matrix method
The transmission-line matrix (TLM) method is a space and time discretising method for computation of electromagnetic fields. It is based on the analogy between the electromagnetic field and a mesh of transmission lines. The TLM method allows the computation of complex three-dimensional electromagnetic structures and has proven to be one of the most powerful time-domain methods along with the finite difference time domain (FDTD) method.
Basic principle

The TLM method is based on Huygens' model of wave propagation and scattering and the analogy between field propagation and transmission lines. Therefore it considers the computational domain as a mesh of transmission lines, interconnected at nodes. In the figure on the right is considered a simple example of a 2D TLM mesh with a voltage pulse of amplitude 1 V incident on the central node. This pulse will be partially reflected and transmitted according to the transmission-line theory. If we assume that each line has a characteristic impedance 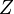 , then the incident pulse sees effectively three transmission lines in parallel with a total impedance of
, then the incident pulse sees effectively three transmission lines in parallel with a total impedance of 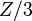 . The reflection coefficient and the transmission coefficient are given by
. The reflection coefficient and the transmission coefficient are given by
The energy injected into the node by the incident pulse and the total energy of the scattered pulses are correspondingly
Therefore the energy conservation law is fulfilled by the model.
The next scattering event excites the neighbouring nodes according to the principle described above. It can be seen that every node turns into a secondary source of spherical wave. These waves combine to form the overall waveform. This is in accordance with Huygens principle of light propagation.
In order to show the TLM schema we will use time and space discretisation. The time-step will be denoted with  and the space discretisation intervals with
and the space discretisation intervals with 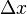 ,
,  and
and  . The absolute time and space will therefore be
. The absolute time and space will therefore be 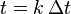 ,
, 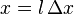 ,
, 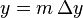 ,
, 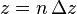 , where
, where 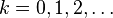 is the time instant and
is the time instant and 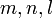 are the cell coordinates. In case
are the cell coordinates. In case 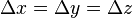 the value
the value 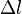 will be used, which is the lattice constant. In this case the following holds:
will be used, which is the lattice constant. In this case the following holds:
where  is the free space speed of light.
is the free space speed of light.
The 2D TLM node
The scattering matrix of an 2D TLM node

If we consider an electromagnetic field distribution in which the only non-zero components are 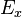 ,
,  and
and 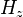 (i.e. a TE-mode distribution), then Maxwell's equations in Cartesian coordinates reduce to
(i.e. a TE-mode distribution), then Maxwell's equations in Cartesian coordinates reduce to
We can combine these equations to obtain
The figure on the right presents a structure referred to as a series node. It describes a block of space dimensions 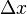 ,
,  and
and  that consists of four ports.
that consists of four ports.  and
and  are the distributed inductance and capacitance of the transmission lines. It is possible to show that a series node is equivalent to a TE-wave, more precisely the mesh current I, the x-direction voltages (ports 1 and 3) and the y-direction voltages (ports 2 and 4) may be related to the field components
are the distributed inductance and capacitance of the transmission lines. It is possible to show that a series node is equivalent to a TE-wave, more precisely the mesh current I, the x-direction voltages (ports 1 and 3) and the y-direction voltages (ports 2 and 4) may be related to the field components 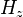 ,
, 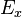 and
and  . If the voltages on the ports are considered,
. If the voltages on the ports are considered,  , and the polarity from the above figure holds, then the following is valid
, and the polarity from the above figure holds, then the following is valid
where 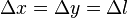 .
.
and dividing both sides by 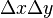
Since 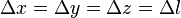 and substituting
and substituting 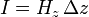 gives
gives
This reduces to Maxwell's equations when 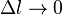 .
.
Similarly, using the conditions across the capacitors on ports 1 and 4, it can be shown that the corresponding two other Maxwell equations are the following:
Having these results, it is possible to compute the scattering matrix of a shunt node. The incident voltage pulse on port 1 at time-step k is denoted as 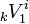 . Replacing the four line segments from the above figure with their Thevenin equivalent it is possible to show that the following equation for the reflected voltage pulse holds:
. Replacing the four line segments from the above figure with their Thevenin equivalent it is possible to show that the following equation for the reflected voltage pulse holds:
If all incident waves as well as all reflected waves are collected in one vector, then this equation may be written down for all ports in matrix form:
where 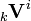 and
and 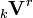 are the incident and the reflected pulse amplitude vectors.
are the incident and the reflected pulse amplitude vectors.
For a series node the scattering matrix S has the following form
Connection between TLM nodes
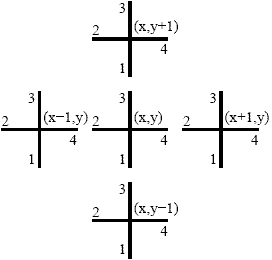
In order to describe the connection between adjacent nodes by a mesh of series nodes, look at the figure on the right. As the incident pulse in timestep k+1 on a node is the scattered pulse from an adjacent node in timestep k, the following connection equations are derived:
By modifying the scattering matrix 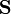 inhomogeneous and lossy materials can be modelled. By adjusting the connection equations it is possible to simulate different boundaries.
inhomogeneous and lossy materials can be modelled. By adjusting the connection equations it is possible to simulate different boundaries.
The shunt TLM node
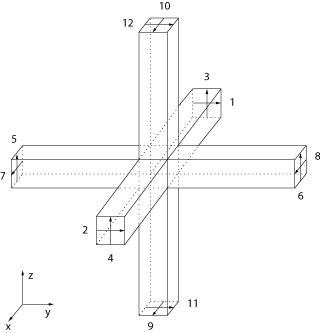
Apart from the series node, described above there is also the shunt TLM node, which represents a TM-mode field distribution. The only non-zero components of such wave are 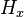 ,
, 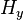 , and
, and 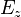 . With similar considerations as for the series node the scattering matrix of the shunt node can be derived.
. With similar considerations as for the series node the scattering matrix of the shunt node can be derived.
3D TLM models
Most problems in electromagnetics require a three-dimensional grid. As we now have structures that describe TE and TM-field distributions, intuitively it seems possible to define a combination of shunt and series nodes providing a full description of the electromagnetic field. Such attempts have been made, but because of the complexity of the resulting structures they proved to be not very useful. Using the analogy that was presented above leads to calculation of the different field components at physically separated points. This causes difficulties in providing simple and efficient boundary definitions. A solution to these problems was provided by Johns in 1987, when he proposed the structure known as the symmetrical condensed node (SCN), presented in the figure on the right. It consists of 12 ports because two field polarisations are to be assigned to each of the 6 sides of a mesh cell.
The topology of the SCN cannot be analysed using Thevenin equivalent circuits. More general energy and charge conservation principles are to be used.
The electric and the magnetic fields on the sides of the SCN node number (l,m,n) at time instant k may be summarised in 12-dimensional vectors
They can be linked with the incident and scattered amplitude vectors via
where 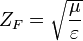 is the field impedance,
is the field impedance, 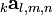 is the vector of the amplitudes of the incident waves to the node, and
is the vector of the amplitudes of the incident waves to the node, and 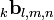 is the vector of the scattered amplitudes. The relation between the incident and scattered waves is given by the matrix equation
is the vector of the scattered amplitudes. The relation between the incident and scattered waves is given by the matrix equation
The scattering matrix S can be calculated. For the symmetrical condensed node with ports defined as in the figure the following result is obtained
where the following matrix was used
The connection between different SCNs is done in the same manner as for the 2D nodes.
References
- C. Christopoulos, The Transmission Line Modeling Method: TLM, Piscataway, NY, IEEE Press, 1995. ISBN 978-0-19-856533-8
- Russer, P., Electromagnetics, Microwave Circuit and Antenna Design for Communications Engineering, Second edition, Artec House, Boston, 2006, ISBN 978-1-58053-907-4
- P. B. Johns and M.O'Brien. "Use of the transmission line modelling (t.l.m) method to solve nonlinear lumped networks", The Radio Electron and Engineer. 1980.
- J. L. Herring, Developments in the Transmission-Line Modelling Method for Electromagnetic Compatibility Studies, PhD thesis, University of Nottingham, 1993.
- Mansour Ahmadian, Transmission Line Matrix (TLM) modelling of medical ultrasound PhD thesis, University of Edinburgh 2001
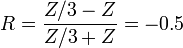
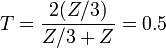
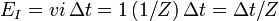
 = \Delta t/Z](../I/m/f5e7d104fa23abcfae90c28f1713ab00.png)
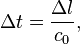
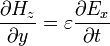
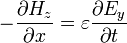
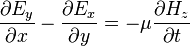
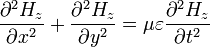
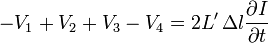
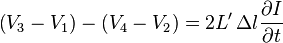
![\left[E_x(y+\Delta y)-E_x(y)\right]\,\Delta x-[E_y(x+\Delta x)-E_y(x)]\Delta y = 2L'\,\Delta l\frac{\partial{I}}{\partial{t}}](../I/m/7c6bbf2a68050b97df7cecb458714ec4.png)
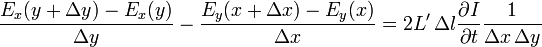
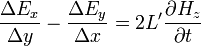
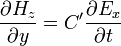
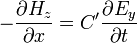
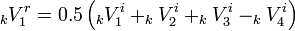
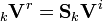
![\mathbf{S}=\frac12\left[
\begin{array}{cccc}
1& 1& 1& -1\\
1& 1& -1& 1\\
1& -1& 1& 1\\
-1& 1& 1& 1
\end{array}
\right]](../I/m/e840f29a9d7b35da927d2a73ea7027f6.png)
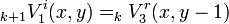
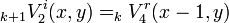
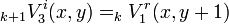
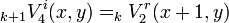
![_k\mathbf{E}_{l,m,n}=_k\left[E_1,E_2,\ldots,E_{11},E_{12}\right]^T_{l,m,n}](../I/m/a034af3fdec5cb09b31e0d5b69254a82.png)
![_k\mathbf{H}_{l,m,n}=_k\left[H_1,H_2,\ldots,H_{11},H_{12}\right]^T_{l,m,n}](../I/m/5b2b03a6080ec70fa4036e6653d98412.png)
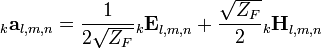
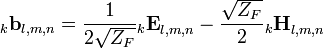
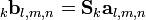
![\mathbf{S} = \left[
\begin{array}{ccc}
0& \mathbf{S}_0& \mathbf{S}^T_0\\
\mathbf{S}^T_0& 0& \mathbf{S}_0\\
\mathbf{S}_0& \mathbf{S}^T_0& 0
\end{array}\right]](../I/m/25e4bac3b24a634a779e3814cd3bf2e2.png)
![\mathbf{S}_0 = \frac{1}{2}\left[
\begin{array}{cccc}
0& 0& 1& -1\\
0& 0& -1& 1\\
1& 1& 0& 0\\
1& 1& 0& 0
\end{array}\right]](../I/m/9d6a8d3af4b98565b19b7b8f48ec5d11.png)