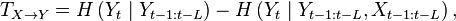Transfer entropy
Transfer entropy is a non-parametric statistic measuring the amount of directed (time-asymmetric) transfer of information between two random processes.[1][2][3] Transfer entropy from a process X to another process Y is the amount of uncertainty reduced in future values of Y by knowing the past values of X given past values of Y. More specifically, if  and
and 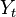 for
for 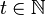 denote two random processes and the amount of information is measured using Shannon's entropy, the transfer entropy can be written as:
denote two random processes and the amount of information is measured using Shannon's entropy, the transfer entropy can be written as:
where H(X) is Shannon entropy of X. The above definition of transfer entropy has been extended by other types of entropy measures such as Rényi entropy.[3]
Transfer entropy is conditional mutual information,[4][5] with the history of the influenced variable 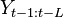 in the condition. Transfer entropy reduces to Granger causality for vector auto-regressive processes.[6] Hence, it is advantageous when the model assumption of Granger causality doesn't hold, for example, analysis of non-linear signals.[7][8] However, it usually requires more samples for accurate estimation.[9]
While it was originally defined for bivariate analysis, transfer entropy has been extended to multivariate forms, either conditioning on other potential source variables[10] or considering transfer from a collection of sources,[11] although these forms require more samples again.
in the condition. Transfer entropy reduces to Granger causality for vector auto-regressive processes.[6] Hence, it is advantageous when the model assumption of Granger causality doesn't hold, for example, analysis of non-linear signals.[7][8] However, it usually requires more samples for accurate estimation.[9]
While it was originally defined for bivariate analysis, transfer entropy has been extended to multivariate forms, either conditioning on other potential source variables[10] or considering transfer from a collection of sources,[11] although these forms require more samples again.
Transfer entropy has been used for estimation of functional connectivity of neurons[11][12] and social influence in social networks.[7]
See also
- Conditional mutual information
- Causality
- Causality (physics)
- Structural equation modeling
- Rubin causal model
- Mutual Information
References
- ↑ Schreiber, Thomas (1 July 2000). "Measuring Information Transfer". Physical Review Letters 85 (2): 461–464. doi:10.1103/PhysRevLett.85.461.
- ↑ Seth, Anil (2007). "Granger causality". Scholarpedia. doi:10.4249/scholarpedia.1667.
- 1 2 Hlaváčková-Schindler, Katerina; PALUS, M; VEJMELKA, M; BHATTACHARYA, J (1 March 2007). "Causality detection based on information-theoretic approaches in time series analysis". Physics Reports 441 (1): 1–46. doi:10.1016/j.physrep.2006.12.004.
- ↑ Wyner, A. D. (1978). "A definition of conditional mutual information for arbitrary ensembles". Information and Control 38 (1): 51–59. doi:10.1016/s0019-9958(78)90026-8.
- ↑ Dobrushin, R. L. (1959). "General formulation of Shannon's main theorem in information theory". Ushepi Mat. Nauk. 14: 3–104.
- ↑ Barnett, Lionel (1 December 2009). "Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables". Physical Review Letters 103 (23). doi:10.1103/PhysRevLett.103.238701.
- 1 2 Ver Steeg, Greg; Galstyan, Aram (2012). "Information transfer in social media". Proceedings of the 21st international conference on World Wide Web (WWW '12). ACM. pp. 509–518.
- ↑ LUNGARELLA, M.; ISHIGURO, K.; KUNIYOSHI, Y.; OTSU, N. (1 March 2007). "METHODS FOR QUANTIFYING THE CAUSAL STRUCTURE OF BIVARIATE TIME SERIES". International Journal of Bifurcation and Chaos 17 (03): 903–921. doi:10.1142/S0218127407017628.
- ↑ Pereda, E; Quiroga, RQ; Bhattacharya, J (Sep–Oct 2005). "Nonlinear multivariate analysis of neurophysiological signals.". Progress in neurobiology 77 (1-2): 1–37. doi:10.1016/j.pneurobio.2005.10.003. PMID 16289760.
- ↑ Lizier, Joseph; Prokopenko, Mikhail; Zomaya, Albert (2008). "Local information transfer as a spatiotemporal filter for complex systems". Physical Review E 77 (2): 026110. doi:10.1103/PhysRevE.77.026110.
- 1 2 Lizier, Joseph; Heinzle, Jakob; Horstmann, Annette; Haynes, John-Dylan; Prokopenko, Mikhail (2011). "Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity". Journal of Computational Neuroscience 30 (1): 85–107. doi:10.1007/s10827-010-0271-2.
- ↑ Vicente, Raul; Wibral, Michael; Lindner, Michael; Pipa, Gordon (February 2011). "Transfer entropy—a model-free measure of effective connectivity for the neurosciences". Journal of Computational Neuroscience 30 (1): 45–67. doi:10.1007/s10827-010-0262-3.
External links
- "Transfer Entropy Toolbox". Google Code., a toolbox, developed in C++ and MATLAB, for computation of transfer entropy between spike trains.
- "Java Information Dynamics Toolkit (JIDT)". Google Code., a toolbox, developed in Java and usable in MATLAB, GNU Octave and Python, for computation of transfer entropy and related information-theoretic measures in both discrete and continuous-valued data.