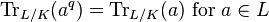Field trace

For other uses, see Trace

In mathematics, the field trace is a particular function defined with respect to a finite field extension L/K, which is a K-linear map from L to K.

Definition

Let K be a field and L a finite extension (and hence an algebraic extension) of K. L can be viewed as a vector space over K. Multiplication by α, an element of L,

m_\alpha:L\to L \text{ given by } m_\alpha (x) = \alpha x

is a K-linear transformation of this vector space into itself. The trace, Tr_L/K(α), is defined as the (linear algebra) trace of this linear transformation.^[1]

For α in L, let σ₁(α), ..., σ_n(α) be the roots (counted with multiplicity) of the minimal polynomial of α over K (in some extension field of L), then

\operatorname{Tr}_{L/K}(\alpha)=[L:K(\alpha)]\sum_{j=1}^n\sigma_j(\alpha)

If L/K is separable then each root appears only once and the coefficient above is one.^[2]

More particularly, if L/K is a Galois extension and α is in L, then the trace of α is the sum of all the Galois conjugates of α, i.e.

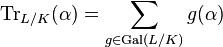\operatorname{Tr}_{L/K}(\alpha)=\sum_{g\in\operatorname{Gal}(L/K)}g(\alpha)

where Gal(L/K) denotes the Galois group of L/K.

Example

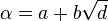Let $L = \mathbb{Q}(\sqrt{d})$ be a quadratic extension of $\mathbb{Q}$ . Then a basis of $L/\mathbb{Q} \text{ is }\{1, \sqrt{d}\}.$ If $\alpha = a + b\sqrt{d}$ then the matrix of $m_{\alpha}$ is:

\left [ \begin{matrix} a & bd \\ b & a \end{matrix} \right ]

and so, $\operatorname{Tr}_{L/\mathbb{Q}}(\alpha) = 2a$ .^[1] The minimal polynomial of α is X² - 2a X + a² - d b².

Properties of the trace

Several properties of the trace function hold for any finite extension.^[3]

The trace Tr_L/K : L → K is a K-linear map (a K-linear functional), that is

\operatorname{Tr}_{L/K}(\alpha a + \beta b) = \alpha \operatorname{Tr}_{L/K}(a)+ \beta \operatorname{Tr}_{L/K}(b) \text{ for all }\alpha, \beta \in K

If α ∈ K then $\operatorname{Tr}_{L/K}(\alpha) = [L:K] \alpha.$

Additionally, trace behaves well in towers of fields: if M is a finite extension of L, then the trace from M to K is just the composition of the trace from M to L with the trace from L to K, i.e.

\operatorname{Tr}_{M/K}=\operatorname{Tr}_{L/K}\circ\operatorname{Tr}_{M/L}

Finite fields

Let L = GF(qⁿ) be a finite extension of a finite field K = GF(q). Since L/K is a Galois extension, if α is in L, then the trace of α is the sum of all the Galois conjugates of α, i.e.^[4]

\operatorname{Tr}_{L/K}(\alpha)=\alpha + \alpha^q + \cdots + \alpha^{q^{n-1}}

In this setting we have the additional properties,^[5]

$\operatorname{Tr}_{L/K}(a^q) = \operatorname{Tr}_{L/K}(a) \text{ for } a \in L$
$\text{for any }\alpha \in K, \text{ we have }|\{b \in L \colon \operatorname{Tr}_{L/K}(b) = \alpha \}| = q^{n-1}$

Theorem.^[6] For b ∈ L, let F_b be the map $a \mapsto \operatorname{Tr}_{L/K}(ba).$ Then F_b ≠ F_c if b ≠ c. Moreover the K-linear transformations from L to K are exactly the maps of the form F_b as b varies over the field L.

When K is the prime subfield of L, the trace is called the absolute trace and otherwise it is a relative trace.^[4]

Application

A quadratic equation, 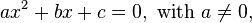$ax^2 + bx + c = 0, \text{ with }a \ne 0,$ and coefficients in the finite field $\operatorname{GF}(q) = \mathbb{F}_q$ has either 0, 1 or 2 roots in GF(q) (and two roots, counted with multiplicity, in the quadratic extension GF(q²)). If the characteristic of GF(q) is odd, the discriminant, Δ = b² - 4ac indicates the number of roots in GF(q) and the classical quadratic formula gives the roots. However, when GF(q) has even characteristic (i.e., q = 2^h for some positive integer h), these formulas are no longer applicable.

Consider the quadratic equation ax² + bx + c = 0 with coefficients in the finite field GF(2^h).^[7] If b = 0 then this equation has the unique solution $x = \sqrt{\frac{c}{a}}$ in GF(q). If b ≠ 0 then the substitution y = ax/b converts the quadratic equation to the form:

y^2 + y + \delta = 0, \text { where } \delta = \frac{ac}{b^2}

This equation has two solutions in GF(q) if and only if the absolute trace $\operatorname{Tr}_{GF(q)/GF(2)}(\delta) = 0.$ In this case, if y = s is one of the solutions, then y = s + 1 is the other. Let k be any element of GF(q) with $\operatorname{Tr}_{GF(q)/GF(2)}(k) = 1.$ Then a solution to the equation is given by:

y = s = k \delta^2 + (k + k^2)\delta^4 + \ldots + (k + k^2 + \ldots + k^{2^{h-2}})\delta^{2^{h-1}}

When h = 2m + 1, a solution is given by the simpler expression:

y = s = \delta + \delta^{2^2} + \delta^{2^4} + \ldots + \delta^{2^{2m}}

Trace form

When L/K is separable, the trace provides a duality theory via the trace form: the map from L × L to K sending (x, y) to Tr_L/K(xy) is a nondegenerate, symmetric, bilinear form called the trace form. An example of where this is used is in algebraic number theory in the theory of the different ideal.

The trace form for a finite degree field extension L/K has non-negative signature for any field ordering of K.^[8] The converse, that every Witt equivalence class with non-negative signature contains a trace form, is true for algebraic number fields K.^[8]

If L/K is an inseparable extension, then the trace form is identically 0.^[9]

Notes

1 2 Rotman 2002, p. 940
↑ Rotman 2002, p. 941
↑ Roman 1995, p. 151 (1st ed.)
1 2 Lidl & Niederreiter 1997, p.54
↑ Mullen & Panario 2013, p. 21
↑ Lidl & Niederreiter 1997, p.56
↑ Hirschfeld 1979, pp. 3-4
1 2 Lorenz (2008) p.38
↑ Isaacs 1994, p. 369 as footnoted in Rotman 2002, p. 943

References

Hirschfeld, J.W.P. (1979), Projective Geometries over Finite Fields, Oxford Mathematical Monographs, Oxford University Press, ISBN 0-19-853526-0
Isaacs, I.M. (1994), Algebra, A Graduate Course, Brooks/Cole Publishing
Lidl, Rudolf; Niederreiter, Harald (1997) [1983], Finite Fields, Encyclopedia of Mathematics and its Applications 20 (Second ed.), Cambridge University Press, ISBN 0-521-39231-4, Zbl 0866.11069
Lorenz, Falko (2008). Algebra. Volume II: Fields with Structure, Algebras and Advanced Topics. Springer. ISBN 978-0-387-72487-4. Zbl 1130.12001.
Mullen, Gary L.; Panario, Daniel (2013), Handbook of Finite Fields, CRC Press, ISBN 978-1-4398-7378-6
Roman, Steven (2006), Field theory, Graduate Texts in Mathematics 158 (Second ed.), Springer, Chapter 8, ISBN 978-0-387-27677-9, Zbl 1172.12001
Rotman, Joseph J. (2002), Advanced Modern Algebra, Prentice Hall, ISBN 978-0-13-087868-7