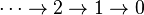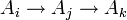Tower (mathematics)
In category theory, a branch of abstract mathematics, a tower is defined as follows. Let 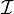 be the poset
be the poset
of whole numbers in reverse order, regarded as a category. A (countable) tower of objects in a category  is a functor from
is a functor from 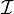 to
to  .
.
In other words, a tower (of  ) is a family of objects
) is a family of objects 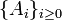 in
in  where there exists a map
where there exists a map
 if
if 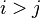
and the composition
is the map 
Example
Let 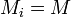 for some
for some  -module
-module 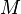 . Let
. Let  be the identity map for
be the identity map for 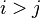 . Then
. Then 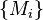 forms a tower of modules.
forms a tower of modules.
References
- Section 3.5 of Weibel, Charles A. (1994), An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics 38, Cambridge University Press, ISBN 978-0-521-55987-4
This article is issued from Wikipedia - version of the Saturday, February 28, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.