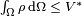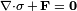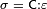Topology optimization
Topology optimization is a mathematical approach that optimizes material layout within a given design space, for a given set of loads and boundary conditions such that the resulting layout meets a prescribed set of performance targets. Using topology optimization, engineers can find the best concept design that meets the design requirements.
Topology optimization has been implemented through the use of finite element methods for the analysis, and optimization techniques based on the method of moving asymptotes, genetic algorithms, optimality criteria method, level sets,[1] and topological derivatives.
Topology optimization is used at the concept level of the design process to arrive at a conceptual design proposal that is then fine tuned for performance and manufacturability. This replaces time consuming and costly design iterations and hence reduces design development time and overall cost while improving design performance.
In some cases, proposals from a topology optimization, although optimal, may be expensive or infeasible to manufacture. These challenges can be overcome through the use of manufacturing constraints in the topology optimization problem formulation. Using manufacturing constraints, the optimization yields engineering designs that would satisfy practical manufacturing requirements. In some cases Additive manufacturing technologies are used to manufacture complex optimized shapes that would otherwise need manufacturing constraints.
Problem Statement
Mathematically one can pose a generic problem as follows:
Subject to:
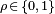
- Design Constraints
- Governing Differential Equation
The problem statement includes the following:
a. Objective functional 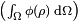 : This is the goal of the optimization study which is to be minimised over the selection field. For example, one would want to minimise the compliance of a structure to increase structural stiffness.
: This is the goal of the optimization study which is to be minimised over the selection field. For example, one would want to minimise the compliance of a structure to increase structural stiffness.
b. Design space 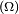 : Design space is the allowable volume within which the design can exist. Assembly and packaging requirements, human and tool accessibility are some of the factors that need to be considered in identifying this space . With the definition of the design space, regions or components in the model that cannot be modified during the course of the optimization are considered as non-design regions.
: Design space is the allowable volume within which the design can exist. Assembly and packaging requirements, human and tool accessibility are some of the factors that need to be considered in identifying this space . With the definition of the design space, regions or components in the model that cannot be modified during the course of the optimization are considered as non-design regions.
c. The Discrete Selection Field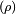 : This is the field over which the discrete optimization is to be performed. It selects or deselects a point on the design space to further the design objective. By selection it has to take the value, 1, and by de-selection it has to take the value, 0.
: This is the field over which the discrete optimization is to be performed. It selects or deselects a point on the design space to further the design objective. By selection it has to take the value, 1, and by de-selection it has to take the value, 0.
d. Design constraints: These are design criteria that need to satisfied. These could include material availability constraints, displacement constraints, etc.
e. Governing Differential Equation: This is the one that governs the physics of the structure to be built. For example the elasticity equation in the case of stiff structures would be the governing differential equation.
Implementation methodology
The optimization problem posed above implies the need for a discrete optimization over every point in domain 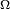 . But, implementation of such a scheme is not yet practicable. So, people adopt continuous optimization strategies, where they assume that the variable
. But, implementation of such a scheme is not yet practicable. So, people adopt continuous optimization strategies, where they assume that the variable  varies continuously over the domain
varies continuously over the domain 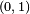 . This problem is then solved over a set of finite elements obtained from meshing of the domain.
. This problem is then solved over a set of finite elements obtained from meshing of the domain.
Topology optimization for stiff structures
A stiff structure is one that has the least possible displacement when given certain set of boundary conditions. A global measure of the displacements is the strain energy (also called compliance) of the structure under the prescribed boundary conditions. The lower the strain energy the higher the stiffness of the structure. So, the problem statement involves the objective functional of the strain energy which has to be minimized.
Now the objective functional should be chosen as a function of the selection field  . So in literature, people have interpolated the material properties in terms of the selection field. A widely used interpolation scheme is called the Solid Isotropic Material with Penalization (SIMP). This interpolation is essentially a power law
. So in literature, people have interpolated the material properties in terms of the selection field. A widely used interpolation scheme is called the Solid Isotropic Material with Penalization (SIMP). This interpolation is essentially a power law 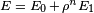 that interpolates the Young's modulus of the material to the scalar selection field. The value of
that interpolates the Young's modulus of the material to the scalar selection field. The value of  varies between
varies between ![\scriptstyle [0,\, 3]](../I/m/bff2e3e6814a483942564c9a012b6914.png) in general. This has been shown to confirm to micro-structure of the materials.[2] So one could view topology optimization to be a process of selection of micro-structure at every point in space so that an objective functional is minimized.
in general. This has been shown to confirm to micro-structure of the materials.[2] So one could view topology optimization to be a process of selection of micro-structure at every point in space so that an objective functional is minimized.
On a broad level, one can visualize that more the material, lesser will be the deflection as there is more material to resist the loads. So, the optimization requires an opposing constraint, the volume constraint . This is in reality a cost factor, as we would not want to spend a lot of money on the material. To obtain the total material utilized, an integration of the selection field over the volume can be done.
Finally the elasticity governing differential equations are plugged in so as to get the final problem statement.
subject to:
But, a straight forward implementation in the Finite Element Framework of such a problem is still infeasible owing to issues such as:
- Mesh dependency—Mesh Dependency means that the design obtained on one mesh is not the one that will be obtained on another mesh. The features of the design become more intricate as the mesh gets refined.
- Numerical instabilities—The selection of region in the form of a chess board.

Some techniques such as Filtering based on Image Processing are currently being used to alleviate some of these issues.

Nowadays, the programs can run 3D topology optimization problems.

Distinction
Topology optimization is distinct from shape optimization since typically shape optimization methods work in a subset of allowable shapes which have fixed topological properties, such as having a fixed number of holes in them. Therefore topology optimization is used to generate concepts and shape optimization is used to fine-tune a chosen design topology.
There are various methods used to perform topology optimization:
- Solid Isotropic Material with Penalisation (SIMP),
- Evolutionary Structural Optimization (ESO),
- Topological derivatives.
List of software performing topology optimization
- Hyperworks Optistruct by Altair[3]
- SolidThinking Inspire by Altair[4]
- Abaqus Tosca Structure, by Dassault Systèmes[5]
- Ansys[6]
- CAESS ProTOp[7]
This list is not complete, a wide panel of tools for topology optimization does exist, more technical as thoses upper to the simpliests.[8]
References
- ↑ , a monograph of the subject.
- ↑ , A reference that proved the validity of the interpolation scheme.
- ↑ Altair OptiStruct, OptiStruct Benefits on Altair's website.
- ↑ Inspire 2015 product overview on Solidthinking's website
- ↑ Abaqus topology optimization module on Dassault Systèmes's website
- ↑ Topology Optimization Extension for Ansys
- ↑ "CAESS Software". Caess.eu. 2016-02-02. Retrieved 2016-02-12.
- ↑ Topostruct, a really simple topology optimization program
- An efficient 3D topology optimization code written in Matlab K. Liu and A. Tovar; Int Journal of Structural and Multidisciplinary Optimization, doi:10.1007/s00158-014-1107-x, available from http://top3dap.com
- Investigation into Structural Topology Optimization Problem Formulations, William Renold, lulu.com, 2007.
- Recent Developments in the Commercial Implementation of Topology Optimization; Uwe Schramm, Ming Zhou; IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials: Status and Perspectives, 239–248; 2006 Springer.
- Industrial Implementation and Applications of Topology Optimization and Future Needs; Claus B.W. Pedersen; Peter Allinger; IUTAM Symposium on Topological Design Optimization of Structures, Machines and Materials, 229-238; 2006 Springer.
- A 99 line topology optimization code written in Matlab Ole Sigmund; Int Journal of Structural and Multidisciplinary Optimization, Volume 21, 120-127, 2001 Springer
- Topology optimization of 2D continua for minimum compliance using parallel computing Arash Mahdavi; Balaji Raghavan; Mary Frecker; Int Journal of Structural and Multidisciplinary Optimization, Volume 32, 121-132, 2006 Springer
- Modern Structural Optimization Concepts Applied to Topology Optimization Juan Pablo Leiva; Brian C. Watson and Iku Kosaka ; 40th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Material Conference. St. Louis, MO, pp. 1589–1596, 1999
- ToPy, an open source topology optimization program written in Python.
External links
- - page containing information on the SIMP optimization method.
- Topology optimization animations
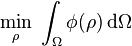
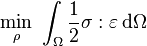
![\scriptstyle \rho \,\in\, [0,\, 1]](../I/m/7c3e5176c7446e968834cbad17cbdf7d.png)