Topological insulator

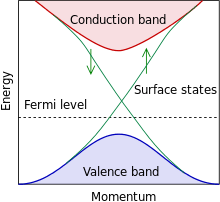
An idealized band structure for a topological insulator. The Fermi level falls within the bulk band gap which is traversed by topologically-protected surface states.

A topological insulator is a material with non-trivial topological order that behaves as an insulator in its interior but whose surface contains conducting states,[1] meaning that electrons can only move along the surface of the material. However, the conducting surface is not the unique character of topological insulator, since the ordinary band insulators can also support conductive surface states. What is special is that the surface states of topological insulators are symmetry protected[2][3][4] by particle number conservation and time reversal symmetry.

In the bulk of a non-interacting topological insulator, the electronic band structure resembles an ordinary band insulator, with the Fermi level falling between the conduction and valence bands. On the surface of a topological insulator there are special states that fall within the bulk energy gap and allow surface metallic conduction. Carriers in these surface states have their spin locked at a right-angle to their momentum (spin-momentum locking). At a given energy the only other available electronic states have different spin, so the "U"-turn scattering is strongly suppressed and conduction on the surface is highly metallic. Non-interacting topological insulators are characterized by an index (known as Z2 topological invariants) similar to the genus in topology.[1]

The "protected" conducting states in the surface are required by time-reversal symmetry and the band structure of the material. The states cannot be removed by surface passivation if it does not break the time-reversal symmetry, which does not happen with potential and/or spin-orbit scattering, but happens in case of true magnetic impurities (e.g. spin-cattering).[5]

Prediction and discovery

Time-reversal symmetry protected edge states were predicted in 1987[6] to occur in quantum wells (very thin layers) of mercury telluride sandwiched between cadmium telluride and were observed in 2007.[7] In 2007, they were predicted[8] to occur in three-dimensional bulk solids of binary compounds involving bismuth. A 3D "strong topological insulator" exists which cannot be reduced to multiple copies of the quantum spin Hall state.[9] The first experimentally realized 3D topological insulator state (symmetry protected surface states) was discovered in bismuth-antimony.[10] Shortly thereafter symmetry protected surface states were also observed in pure antimony, bismuth selenide, bismuth telluride and antimony telluride using ARPES.[11] Many semiconductors within the large family of Heusler materials are now believed to exhibit topological surface states.[12][13] In some of these materials the Fermi level actually falls in either the conduction or valence bands due to naturally occurring defects, and must be pushed into the bulk gap by doping or gating.[14][15] The surface states of a 3D topological insulator is a new type of 2DEG (two-dimensional electron gas) where the electron's spin is locked to its linear momentum.[16]

Fully bulk insulating or intrinsic 3D topological insulator states exist in Bi-based materials (Nature Physics 2014) [17]

In 2012 several groups released preprints which suggest that samarium hexaboride has the properties of a topological insulator[18] in accordance with the earlier theoretical predictions.[19] Since samarium hexaboride is an established Kondo insulator, i.e. a strongly correlated electron material, the existence of a topological surface state in this material would lead to a topological insulator with strong electronic correlations.

Stanene is a theoretical topological insulator which may display superconductivity at its edges above room temperature.

A study published in July 2014 of Nature magazine demonstrates that magnetic components, like the ones in computer memory, can be manipulated by topological insulators.[20][21]

Properties and applications

The spin-momentum locking[16] in the topological insulator allows symmetry protected surface states to host Majorana particles if superconductivity is induced on the surface of 3D topological insulators via proximity effects.[22] (Note that Majorana zero-mode can also appear without topological insulators.[23]) The non-trivialness of topological insulators is encoded in the existence of a gas of helical Dirac fermions. Helical Dirac fermions, which behave like massless relativistic particles, have been observed in 3D topological insulators.

Note that the gapless surface states of topological insulator differ from those in the Quantum Hall effect: the gapless surface states of topological insulator are symmetry protected (i.e. not topological), while the gapless surface states in Quantum Hall effect are topological (i.e. robust against any local perturbations that can break all the symmetries).

The Z2 topological invariants cannot be measured using traditional transport methods, such as spin Hall conductance, and the transport is not quantized by the Z2 invariants. An experimental method to measure Z2 topological invariants was demonstrated which provide a measure of the Z2 topological order.[24] (Note that the term Z2 topological order has also been used to describe the topological order with emergent Z2 gauge theory discovered in 1991.[25][26])

References

  1. 1 2 Kane, C. L.; Mele, E. J. (30 September 2005). "Z2 Topological Order and the Quantum Spin Hall Effect". Physical Review Letters 95 (14): 146802. arXiv:cond-mat/0506581. Bibcode:2005PhRvL..95n6802K. doi:10.1103/PhysRevLett.95.146802.
  2. ↑ Zheng-Cheng Gu and Xiao-Gang Wen Tensor-Entanglement-Filtering Renormalization Approach and Symmetry Protected Topological Order Phys. Rev. B80, 155131 (2009).
  3. ↑ Pollmann, F.; Berg, E.; Turner, Ari M.; Oshikawa, Masaki (2012). "Symmetry protection of topological phases in one-dimensional quantum spin systems". Phys. Rev. B 85 (7): 075125. arXiv:0909.4059. Bibcode:2012PhRvB..85g5125P. doi:10.1103/PhysRevB.85.075125.
  4. ↑ Xie Chen, Zheng-Cheng Gu, Xiao-Gang Wen, Classification of Gapped Symmetric Phases in 1D Spin Systems Phys. Rev. B 83, 035107 (2011); Xie Chen, Zheng-Xin Liu, Xiao-Gang Wen, 2D symmetry protected topological orders and their protected gapless edge excitations Phys. Rev. B 84, 235141 (2011)
  5. ↑ Th. Guhr, A. Müller-Groening, H.A. Weidenmüller: Random Matrix Theories in Quantum Physics: Common Concepts. In: Physics Reports, volume 299, 1998, p. 189–425.
  6. ↑ Pankratov, O.A.; Pakhomov, S.V.; Volkov, B.A. (January 1987). "Supersymmetry in heterojunctions: Band-inverting contact on the basis of Pb1-xSnxTe and Hg1-xCdxTe". Solid State Communications 61 (2): 93–96. Bibcode:1987SSCom..61...93P. doi:10.1016/0038-1098(87)90934-3.
  7. ↑ König, Markus; Wiedmann, Steffen; Brüne, Christoph; Roth, Andreas; Buhmann, Hartmut; Molenkamp, Laurens W.; Qi, Xiao-Liang; Zhang, Shou-Cheng (2007-11-02). "Quantum Spin Hall Insulator State in HgTe Quantum Wells". Science 318 (5851): 766–770. arXiv:0710.0582. Bibcode:2007Sci...318..766K. doi:10.1126/science.1148047. PMID 17885096. Retrieved 2010-03-25.
  8. ↑ Fu, Liang; C. L. Kane (2007-07-02). "Topological insulators with inversion symmetry". Physical Review B 76 (4): 045302. arXiv:cond-mat/0611341. Bibcode:2007PhRvB..76d5302F. doi:10.1103/PhysRevB.76.045302. Retrieved 2010-03-26. Shuichi Murakami (2007). "Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase". New Journal of Physics 9 (9): 356–356. arXiv:0710.0930. Bibcode:2007NJPh....9..356M. doi:10.1088/1367-2630/9/9/356. ISSN 1367-2630. Retrieved 2010-03-26.
  9. ↑ Kane, C. L.; Moore, J. E. (2011). "Topological Insulators" (PDF). Physics World 24: 32.
  10. ↑ Hsieh, David; Dong Qian, Andrew L. Wray, Yuqi Xia, Yusan Hor, Robert Cava & M. Zahid Hasan (2008). "A Topological Dirac insulator in a quantum spin Hall phase". Nature 452 (9): 970–974. arXiv:0902.1356. Bibcode:2008Natur.452..970H. doi:10.1038/nature06843. PMID 18432240. Retrieved 2010. Cite uses deprecated parameter |coauthors= (help)
  11. ↑ Hasan, M. Zahid; Kane, Charles L. (2010). "Topological Insulators". Review of Modern Physics 82 (4): 3045. arXiv:1002.3895. Bibcode:2010RvMP...82.3045H. doi:10.1103/RevModPhys.82.3045. Retrieved 2010-03-25.
  12. ↑ Chadov, Stanislav; Xiao-Liang Qi; Jürgen Kübler; Gerhard H. Fecher; Claudia Felser; Shou-Cheng Zhang (July 2010). "Tunable multifunctional topological insulators in ternary Heusler compounds". Nature Materials 9 (7): 541–545. arXiv:1003.0193. Bibcode:2010NatMa...9..541C. doi:10.1038/nmat2770. Retrieved 2010-08-05.
  13. ↑ Lin, Hsin; L. Andrew Wray; Yuqi Xia; Suyang Xu; Shuang Jia; Robert J. Cava; Arun Bansil; M. Zahid Hasan (July 2010). "Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena". Nat Mater 9 (7): 546–549. arXiv:1003.0155. Bibcode:2010NatMa...9..546L. doi:10.1038/nmat2771. ISSN 1476-1122. PMID 20512153. Retrieved 2010-08-05.
  14. ↑ Hsieh, D.; Y. Xia, D. Qian, L. Wray, F. Meier, J. H. Dil, J. Osterwalder, L. Patthey, A. V. Fedorov, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava, M. Z. Hasan (2009). "Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2Te3 and Sb2Te3". Physical Review Letters 103 (14): 146401. Bibcode:2009PhRvL.103n6401H. doi:10.1103/PhysRevLett.103.146401. PMID 19905585. Retrieved 2010-03-25. Cite uses deprecated parameter |coauthors= (help)
  15. ↑ Noh, H.-J.; H. Koh, S.-J. Oh, J.-H. Park, H.-D. Kim, J. D. Rameau, T. Valla, T. E. Kidd, P. D. Johnson, Y. Hu and Q. Li (2008). "Spin-orbit interaction effect in the electronic structure of Bi2Te3 observed by angle-resolved photoemission spectroscopy". EPL Europhysics Letters 81 (5): 57006. arXiv:0803.0052. Bibcode:2008EL.....8157006N. doi:10.1209/0295-5075/81/57006. Retrieved 2010-04-25. Cite uses deprecated parameter |coauthors= (help)
  16. 1 2 Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Dil, J. H.; Meier, F.; Osterwalder, J.; Patthey, L.; Checkelsky, J. G.; Ong, N. P.; Fedorov, A. V.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y. S.; Cava, R. J.; Hasan, M. Z. (2009). "A tunable topological insulator in the spin helical Dirac transport regime". Nature 460 (7259): 1101–1105. arXiv:1001.1590. Bibcode:2009Natur.460.1101H. doi:10.1038/nature08234. PMID 19620959.
  17. ↑ Xu et.al.,. "Observation of topological surface state quantum Hall effect in an intrinsic three-dimensional topological insulator". Nature Physics 10, 956 (2014). doi:10.1038/nphys3140.
  18. ↑ Eugenie Samuel Reich. "Hopes surface for exotic insulator". Nature.
  19. ↑ Dzero, V.; K. Sun; V. Galitski; P. Coleman (2009). "Topological Kondo Insulators". Physical Review Letters 104 (10): 106408. arXiv:0912.3750. Bibcode:2010PhRvL.104j6408D. doi:10.1103/PhysRevLett.104.106408. Retrieved 2013-01-06.
  20. ↑ "Weird materials could make faster computers". Science News. doi:10.1038/nature13534. Retrieved 2014-07-23.
  21. ↑ http://www.nature.com/nature/journal/v511/n7510/full/nature13534.html
  22. ↑ Fu, L.; C. L. Kane (2008). "Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator". Phys. Rev. Lett. 100: 096407. arXiv:0707.1692. Bibcode:2008PhRvL.100i6407F. doi:10.1103/PhysRevLett.100.096407. Retrieved 2010.
  23. ↑ Topological Superconductivity and Majorana Fermions in Metallic Surface-States Andrew C. Potter, Patrick A. Lee, Phys. Rev. B 85, 094516 (2012) arXiv:1201.2176
  24. ↑ Hsieh, D.; D. Hsieh, Y. Xia, L. Wray, D. Qian, A. Pal, J. H. Dil, F. Meier, J. Osterwalder, C. L. Kane, G. Bihlmayer, Y. S. Hor, R. J. Cava and M. Z. Hasan (2009). "Observation of Unconventional Quantum Spin Textures in Topological Insulators". Science 323 (5916): 919–922. Bibcode:2009Sci...323..919H. doi:10.1126/science.1167733. Retrieved 2010. Cite uses deprecated parameter |coauthors= (help)
  25. ↑ N. Read and Subir Sachdev, Large-N expansion for frustrated quantum antiferromagnets, Phys. Rev. Lett. 66 1773 (1991)
  26. ↑ Xiao-Gang Wen, Mean Field Theory of Spin Liquid States with Finite Energy Gaps, Phys. Rev. B 44 2664 (1991).

Further reading

This article is issued from Wikipedia - version of the Wednesday, January 20, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.