Toda–Smith complex
In mathematics, Toda–Smith complexes are spectra characterized by having a particularly simple homology, and are used in stable homotopy theory.
Toda–Smith complexes provided examples of periodic maps. Thus, they led to the construction of the nilpotent and periodicity theorems,[1] which provided the first organization of the stable homotopy groups of spheres into families of maps localized at a prime.
Mathematical context
The story begins with the degree  map on
map on  (as a circle in the complex plane):
(as a circle in the complex plane):
The degree  map is well defined for
map is well defined for  in general, where
in general, where  .
If we apply the infinite suspension functor to this map,
.
If we apply the infinite suspension functor to this map, 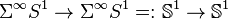 and we take the cofiber of the resulting map:
and we take the cofiber of the resulting map:
We find that 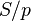 has the remarkable property of coming from a Moore space (i.e., a designer (co)homology space:
has the remarkable property of coming from a Moore space (i.e., a designer (co)homology space: 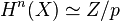 , and
, and 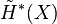 is trivial for all
is trivial for all 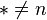 ).
).
It is also of note that the periodic maps, 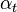 ,
, 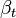 , and
, and 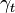 , come from degree maps between the Toda–Smith complexes,
, come from degree maps between the Toda–Smith complexes, 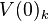 ,
, 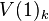 , and
, and 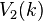 respectively.
respectively.
Formal definition
The  th Toda–Smith complex,
th Toda–Smith complex, 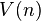 where
where 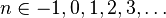 , is a finite spectrum which satisfies the property that its BP-homology,
, is a finite spectrum which satisfies the property that its BP-homology, ![BP_*(V(n)) := [\mathbb{S}^0, BP \wedge V(n)]](../I/m/734b28343d0beb546dc729f76d4cc3ce.png) , is isomorphic to
, is isomorphic to 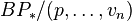 .
.
That is, Toda–Smith complexes are completely characterized by their 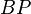 -local properties, and are defined as any object
-local properties, and are defined as any object 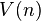 satisfying one of the following equations:
satisfying one of the following equations:
It may help the reader to recall that that ![BP_* = \mathbb{Z}_p[v_1, v_2, ...]](../I/m/90e59e0890a36a1c25fd47e24c49cc9e.png) ,
, 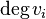 =
= 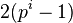 .
.
Examples of Toda–Smith complexes
- the sphere spectrum,
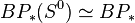 , which is
, which is 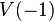 .
. - the mod p Moore spectrum,
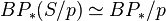 , which is
, which is 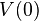
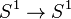
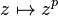
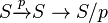
![\begin{align}
BP_*(V(-1)) & \simeq BP_* \\[6pt]
BP_*(V(0)) & \simeq BP_*/p \\[6pt]
BP_*(V(1)) & \simeq BP_*/(p, v_1) \\[2pt]
& {}\,\,\,\vdots
\end{align}](../I/m/f5edc5a70348146dacd61b85a11718ec.png)