Reversible computing

Reversible computing is a model of computing where the computational process to some extent is reversible, i.e., time-invertible. In a computational model that uses transitions from one state of the abstract machine to another, a necessary condition for reversibility is that the relation of the mapping from states to their successors must be one-to-one. Reversible computing is generally considered an unconventional form of computing.

Reversibility

There are two major, closely related, types of reversibility that are of particular interest for this purpose: physical reversibility and logical reversibility.[1]

A process is said to be physically reversible if it results in no increase in physical entropy; it is isentropic. These circuits are also referred to as charge recovery logic, adiabatic circuits, or adiabatic computing. Although in practice no nonstationary physical process can be exactly physically reversible or isentropic, there is no known limit to the closeness with which we can approach perfect reversibility, in systems that are sufficiently well-isolated from interactions with unknown external environments, when the laws of physics describing the system's evolution are precisely known.

Probably the largest motivation for the study of technologies aimed at actually implementing reversible computing is that they offer what is predicted to be the only potential way to improve the energy efficiency of computers beyond the fundamental von Neumann-Landauer limit[2] of kT ln(2) energy dissipated per irreversible bit operation. (Though even the Landauer limit was millions of times below the energy consumption of computers in 2000-s and thousands less in 2010-s.[3])

Relation to thermodynamics

As was first argued by Rolf Landauer of IBM,[4] in order for a computational process to be physically reversible, it must also be logically reversible. Landauer's principle is the loosely formulated notion that the erasure of n bits of information must always incur a cost of nkT ln(2) in thermodynamic entropy. A discrete, deterministic computational process is said to be logically reversible if the transition function that maps old computational states to new ones is a one-to-one function; i.e. the output logical states uniquely defines the input logical states of the computational operation.

For computational processes that are nondeterministic (in the sense of being probabilistic or random), the relation between old and new states is not a single-valued function, and the requirement needed to obtain physical reversibility becomes a slightly weaker condition, namely that the size of a given ensemble of possible initial computational states does not decrease, on average, as the computation proceeds forwards.

Physical reversibility

Landauer's principle (and indeed, the second law of thermodynamics itself) can also be understood to be a direct logical consequence of the underlying reversibility of physics, as is reflected in the general Hamiltonian formulation of mechanics, and in the unitary time-evolution operator of quantum mechanics more specifically.

The implementation of reversible computing thus amounts to learning how to characterize and control the physical dynamics of mechanisms to carry out desired computational operations so precisely that we can accumulate a negligible total amount of uncertainty regarding the complete physical state of the mechanism, per each logic operation that is performed. In other words, we would need to precisely track the state of the active energy that is involved in carrying out computational operations within the machine, and design the machine in such a way that the majority of this energy is recovered in an organized form that can be reused for subsequent operations, rather than being permitted to dissipate into the form of heat.

Although achieving this goal presents a significant challenge for the design, manufacturing, and characterization of ultra-precise new physical mechanisms for computing, there is at present no fundamental reason to think that this goal cannot eventually be accomplished, allowing us to someday build computers that generate much less than 1 bit's worth of physical entropy (and dissipate much less than kT ln 2 energy to heat) for each useful logical operation that they carry out internally.

Today, the field has a substantial body of academic literature behind it. A wide variety of reversible device concepts, logic gates, electronic circuits, processor architectures, programming languages, and application algorithms have been designed and analyzed by physicists, electrical engineers, and computer scientists.

This field of research awaits the detailed development of a high-quality, cost-effective, nearly reversible logic device technology, one that includes highly energy-efficient clocking and synchronization mechanisms. This sort of solid engineering progress will be needed before the large body of theoretical research on reversible computing can find practical application in enabling real computer technology to circumvent the various near-term barriers to its energy efficiency, including the von Neumann-Landauer bound. This may only be circumvented by the use of logically reversible computing, due to the Second Law of Thermodynamics.

Logical Reversibility

To implement reversible computation, estimate its cost, and to judge its limits, it is formalized in terms of gate-level circuits. For example, the inverter (logic gate) (NOT) gate is reversible because it can be undone. The exclusive or (XOR) gate is irreversible because its two inputs cannot be unambiguously reconstructed from its single output. However, a reversible version of the XOR gate—the controlled NOT gate (CNOT)—can be defined by preserving one of the inputs. The three-input variant of the CNOT gate is called the Toffoli gate. It preserves two of its inputs a,b and replaces the third c by c\oplus (a\cdot b). 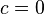With c=0, this gives the AND function, and with a\cdot b=1 this gives the NOT function. Thus, the Toffoli gate is universal and can implement any reversible Boolean function (given enough zero-initialized ancillary bits). More generally, reversible gates have the same number of inputs and outputs. A reversible circuit connects reversible gates without fanouts and loops. Therefore, such circuits contain equal numbers of input and output wires, each going through an entire circuit. Similarly, in the Turing machine model of computation, a reversible Turing machine is one whose transition function is invertible, so that each machine state has at most one predecessor.

Yves Lecerf proposed a reversible Turing machine in a little-noticed 1963 paper,[5] but apparently unaware of Landauer's principle, did not pursue the subject further, devoting most of the rest of his career to ethnolinguistics. In 1973 Bennett, at IBM Research, showed that a universal Turing machine could be made both logically and thermodynamically reversible,[6] and therefore able in principle perform arbitrarily much computation per unit of physical energy dissipated, in the limit of zero speed. In 1982 Fredkin and Toffoli proposed the Billiard ball computer, a mechanism using classical hard spheres to do reversible computations at finite speed with zero dissipation, but requiring perfect initial alignment of the balls' trajectories, and Bennett's review[7] compared these "Brownian" and "ballistic" paradigms for reversible computation. Aside from the motivation of energy-efficient computation, reversible logic gates offered practical improvements of bit-manipulation transforms in cryptography and computer graphics. Since the 1980s, reversible circuits have attracted interest as components of quantum algorithms, and more recently in photonic and nano-computing technologies where some switching devices offer no signal gain.

Surveys of reversible circuits, their construction and optimization, as well as recent research challenges, are available.[8][9][10]

See also

References

  1. ↑ http://www.cise.ufl.edu/research/revcomp/
  2. ↑ J. von Neumann, Theory of Self-Reproducing Automata, Univ. of Illinois Press, 1966.
  3. ↑ Bérut, Antoine, et al. "Experimental verification of Landauer/'s principle linking information and thermodynamics." Nature 483.7388 (2012): 187-189: "From a technological perspective, energy dissipation per logic operation in present-day silicon-based digital circuits is about a factor of 1,000 greater than the ultimate Landauer limit, but is predicted to quickly attain it within the next couple of decades"
  4. ↑ R. Landauer, "Irreversibility and heat generation in the computing process," IBM Journal of Research and Development, vol. 5, pp. 183-191, 1961.
  5. ↑ Lecerf (Y.) : Logique Mathématique : Machines de Turing réversibles. Comptes rendus des séances de l'académie des sciences, 257:2597--2600, 1963.
  6. ↑ C. H. Bennett, "Logical reversibility of computation," IBM Journal of Research and Development, vol. 17, no. 6, pp. 525-532, 1973
  7. ↑ C. H. Bennett, "The Thermodynamics of Computation -- A Review," International Journal of Theoretical Physics, vol. 21, no. 12, pp. 905-940, 1982
  8. ↑ Rolf Drechsler, Robert Wille. From Truth Tables to Programming Languages: Progress in the Design of Reversible Circuits. International Symposium on Multiple-Valued Logic, 2011. http://www.informatik.uni-bremen.de/agra/doc/konf/11_ismvl_reversible_circuit_design_tutorial.pdf
  9. ↑ Mehdi Saeedi, Igor L. Markov, Synthesis and Optimization of Reversible Circuits - A Survey, ACM Computing Surveys, 2012. http://arxiv.org/abs/1110.2574
  10. ↑ Rolf Drechsler and Robert Wille. Reversible Circuits: Recent Accomplishments and Future Challenges for an Emerging Technology. International Symposium on VLSI Design and Test, 2012. http://www.informatik.uni-bremen.de/agra/doc/konf/2012_vdat_reversible_circuits_accompl_chall.pdf

Further reading

External links

This article is issued from Wikipedia - version of the Tuesday, January 26, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.