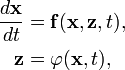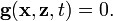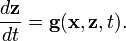Tikhonov's theorem (dynamical systems)

In applied mathematics, Tikhonov's theorem on dynamical systems is a result on stability of solutions of systems of differential equations. It has applications to chemical kinetics.[1] The theorem is named after Andrey Nikolayevich Tikhonov.

Statement

Consider this system of differential equations:

\begin{align} \frac{d\mathbf{x}}{dt} & = \mathbf{f}(\mathbf{x},\mathbf{z},t), \\ \mu\frac{d\mathbf{z}}{dt} & = \mathbf{g}(\mathbf{x},\mathbf{z},t). \end{align}

Taking the limit as 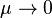\mu\to 0, this becomes the "degenerate system":

\begin{align} \frac{d\mathbf{x}}{dt} & = \mathbf{f}(\mathbf{x},\mathbf{z},t), \\ \mathbf{z} & = \varphi(\mathbf{x},t), \end{align}

where the second equation is the solution of the algebraic equation

\mathbf{g}(\mathbf{x},\mathbf{z},t) = 0. \,

Note that there may be more than one such function φ.

Tikhonov's theorem states that as 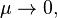\mu\to 0,\, the solution of the system of two differential equations above approaches the solution of the degenerate system if \mathbf{z} = \varphi(\mathbf{x},t) is a stable root of the "adjoined system"

\frac{d\mathbf{z}}{dt} = \mathbf{g}(\mathbf{x},\mathbf{z},t).

References

  1. ↑ http://www.math.bme.hu/~jtoth/frk/Roussel.pdf

External links

This article is issued from Wikipedia - version of the Sunday, February 05, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.