Thiele modulus
The Thiele modulus was developed by E.W. Thiele in his paper 'Relation between catalytic activity and size of particle' in 1939.[1] Thiele reasoned that with a large enough particle, the reaction rate is so rapid that diffusion forces are only able to carry product away from the surface of the catalyst particle. Therefore, only the surface of the catalyst would be experiencing any reaction. The Thiele Modulus was then developed to describe the relationship between diffusion and reaction rate in porous catalyst pellets with no mass transfer limitations. This value is generally used in determining the effectiveness factor for catalyst pellets.
The Thiele modulus is represented by different symbols in different texts, but is defined in Hill[2] as hT.
Overview
The derivation of the Thiele Modulus (from Hill) begins with a material balance on the catalyst pore. For a first-order irreversible reaction in a straight cylindrical pore at steady state:
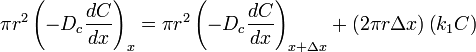
where  is a diffusivity constant, and
is a diffusivity constant, and  is the rate constant.
is the rate constant.
Then, turning the equation into a differential by dividing by 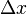 and taking the limit as
and taking the limit as 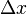 approaches 0,
approaches 0,
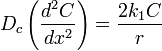
This differential equation with the following boundary conditions:
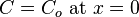
and
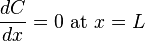
where the first boundary condition indicates a constant external concentration on one end of the pore and the second boundary condition indicates that there is no flow out of the other end of the pore.
Plugging in these boundary conditions, we have
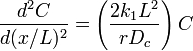
The term on the right side multiplied by C represents the square of the Thiele Modulus, which we now see rises naturally out of the material balance. Then the Thiele modulus for a first order reaction is:
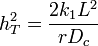
From this relation it is evident that with large values of 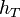 , the rate term dominates, and the reaction is fast while slow diffusion limits the overall rate. Smaller values of the Thiele modulus represent slow reactions with fast diffusion.
, the rate term dominates, and the reaction is fast while slow diffusion limits the overall rate. Smaller values of the Thiele modulus represent slow reactions with fast diffusion.
Other Forms
Other order reactions may be solved in a similar manner as above. The results are listed below for irreversible reactions in straight cylindrical pores.
Second Order Reaction
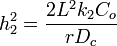
Zeroth Order Reaction
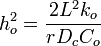
Effectiveness Factor
The effectiveness factor η relates the diffusive reaction rate with the rate of reaction in the bulk stream.
For a first order reaction in a slab geometry,[1][3] this is:
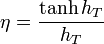
References
- 1 2 Thiele, E.W. Relation between catalytic activity and size of particle. Industrial and Engineering Chemistry, 31 (1939), pp. 916–920
- ↑ Hill, C. An Introduction to Chemical Engineering and Reactor Design. John Wiley & Sons, Inc. 1977, 440-446.
- ↑ Froment, G. F.; et al. (2011). Chemical Reactor Analysis and Design (3rd ed.). John Wiley & Sons. p. 195. ISBN 978-0-470-56541-4.
