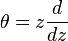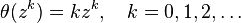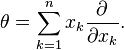Theta operator
In mathematics, the theta operator is a differential operator defined by[1][2]
This is sometimes also called the homogeneity operator, because its eigenfunctions are the monomials in z:
In n variables the homogeneity operator is given by
As in one variable, the eigenspaces of θ are the spaces of homogeneous polynomials.
See also
- Difference operator
- Delta operator
- Elliptic operator
- Fractional calculus
- Invariant differential operator
- Differential calculus over commutative algebras
References
- ↑ "Theta Operator - from Wolfram MathWorld". Mathworld.wolfram.com. Retrieved 2013-02-16.
- ↑ Weisstein, Eric W. (2002). CRC Concise Encyclopedia of Mathematics. (2nd ed.). Hoboken: CRC Press. pp. 2976–2983. ISBN 1420035223.
Further reading
- Watson, G.N. (1995). A treatise on the theory of Bessel functions (Cambridge mathematical library ed., [Nachdr. der] 2. ed.). Cambridge: Univ. Press. ISBN 0521483913.
This article is issued from Wikipedia - version of the Thursday, December 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.