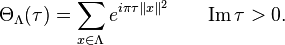Theta function of a lattice
In mathematics, the theta function of a lattice is a function whose coefficients give the number of vectors of a given norm.
Definition
One can associate to any (positive-definite) lattice Λ a theta function given by
The theta function of a lattice is then a holomorphic function on the upper half-plane. Furthermore, the theta function of an even unimodular lattice of rank n is actually a modular form of weight n/2. The theta function of an integral lattice is often written as a power series in 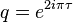 so that the coefficient of qn gives the number of lattice vectors of norm 2n.
so that the coefficient of qn gives the number of lattice vectors of norm 2n.
References
- Deconinck, Bernard (2010), "Multidimensional Theta Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
This article is issued from Wikipedia - version of the Friday, February 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.