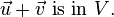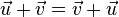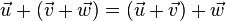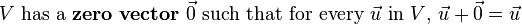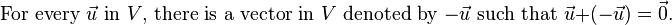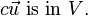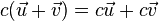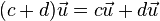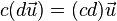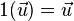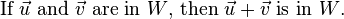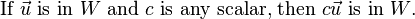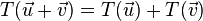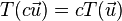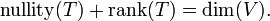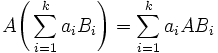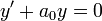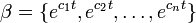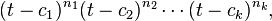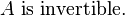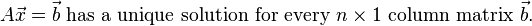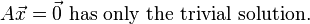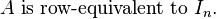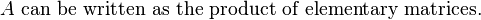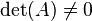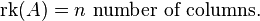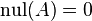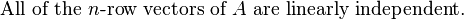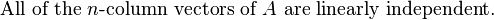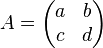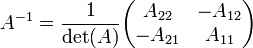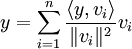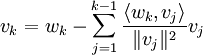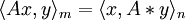Theorems and definitions in linear algebra
This article collects the main theorems and definitions in linear algebra.
Vector Spaces
Let V be a set on which two operations (vector addition and scalar multiplication) are defined. If the listed axioms are satisfied for every  ,
,  , and
, and 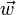 in V and every scalar c and d, then V is called a vector space:
in V and every scalar c and d, then V is called a vector space:
Addition:
Scalar Multiplication:
Subspaces
If W is a nonempty subset of a vector space V, then W is a subspace of V if and only if the following closure conditions hold:
Linear combinations
A vector 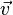 in a vector space V is called a linear combination of the vectors
in a vector space V is called a linear combination of the vectors 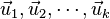 in V if
in V if 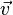 can be written in the form
can be written in the form 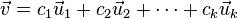 , where
, where 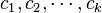 are scalars.
are scalars.
Systems of linear equations
A system of linear equations (or linear system) is a collection of linear equations involving the same set of variables.
Cramer's Rule
If a system of n linear equations in n variables has a coefficient matrix with a nonzero determinant |A|, then the solution of the system is given by
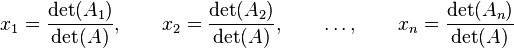 ,
,
where Ai is the matrix A with the i-th column of A replaced by the column of constants in the system of equations.
Linear dependence
A set of vectors 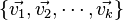 in a vector space V is linearly dependent if there exists a set of scalars, {x1, x2, ..., xk }, not all zero, so that the vector equation
in a vector space V is linearly dependent if there exists a set of scalars, {x1, x2, ..., xk }, not all zero, so that the vector equation 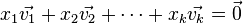 has a solution.
has a solution.
Linear independence
A set of vectors 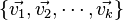 in a vector space V is linearly independent if the vector equation
in a vector space V is linearly independent if the vector equation 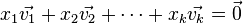 has only the trivial solution,
has only the trivial solution, 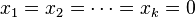 .
.
Bases
A set of vectors 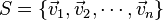 in a vector space V is called a basis if the following conditions are true:
in a vector space V is called a basis if the following conditions are true:
-
 spans
spans  .
. -
 is linearly independent.
is linearly independent.
Linear transformations and matrices
Change of coordinate matrix
Clique
Coordinate vector relative to a basis
Dimension theorem
Dominance relation
Identity matrix
Identity transformation
Incidence matrix
Inverse of a linear transformation
Inverse of a matrix
Invertible linear transformation
Isomorphic vector spaces
Isomorphism
Kronecker delta
Left-multiplication transformation
Linear operator
Linear transformation
Matrix representing a linear transformation
Nullity of a linear transformation
Null space
Ordered basis
Product of matrices
Projection on a subspace
Projection on the x-axis
Range
Rank of a linear transformation
Reflection about the x-axis
Rotation
Similar matrices
Standard ordered basis for 
Standard representation of a vector space with respect to a basis
Zero transformation
P.S. coefficient of the differential equation, differentiability of complex function,vector space of functionsdifferential operator, auxiliary polynomial, to the power of a complex number, exponential function.
Definition of a Linear Transformation
Let  and
and 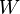 be vector spaces. The function
be vector spaces. The function 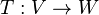 is called a linear transformation of
is called a linear transformation of  into
into 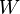 if the following two properties are true for all
if the following two properties are true for all 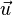 and
and 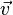 in
in  and for any scalar
and for any scalar  .
.
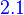 N(T) and R(T) are subspaces
N(T) and R(T) are subspaces
Let V and W be vector spaces and I: V → W be linear. Then N(T) and R(T) are subspaces of V and W, respectively.
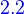 R(T)= span of T(basis in V)
R(T)= span of T(basis in V)
Let V and W be vector spaces, and let T: V→W be linear. If 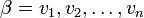 is a basis for V, then
is a basis for V, then
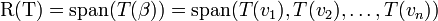 .
.
 Dimension theorem
Dimension theorem
Let V and W be vector spaces, and let T: V → W be linear. If V is finite-dimensional, then
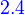 one-to-one ⇔ N(T) = {0}
one-to-one ⇔ N(T) = {0}
Let 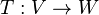 be a linear transformation. Then
be a linear transformation. Then  is one-to-one if and only if
is one-to-one if and only if 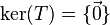 .
.
 one-to-one ⇔ onto ⇔ rank(T) = dim(V)
one-to-one ⇔ onto ⇔ rank(T) = dim(V)
Let V and W be vector spaces of equal (finite) dimension, and let T:V → W be linear. Then the following are equivalent.
- (a) T is one-to-one.
- (b) T is onto.
- (c) rank(T) = dim(V).
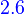 ∀
∀ 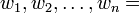 exactly one T (basis),
exactly one T (basis),
Let V and W be vector space over F, and suppose that 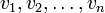 is a basis for V. For
is a basis for V. For 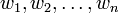 in W, there exists exactly one linear transformation T: V→W such that
in W, there exists exactly one linear transformation T: V→W such that 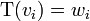 for
for 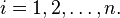
Corollary.
Let V and W be vector spaces, and suppose that V has a finite basis 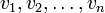 . If U, T: V→W are linear and
. If U, T: V→W are linear and 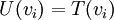 for
for 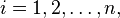 then U=T.
then U=T.
 T is vector space
T is vector space
Let V and W be vector spaces over a field F, and let T, U: V→W be linear.
- (a) For all
 ∈ F,
∈ F, 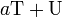 is linear.
is linear. - (b) Using the operations of addition and scalar multiplication in the preceding definition, the collection of all linear transformations form V to W is a vector space over F.
 linearity of matrix representation of linear transformation
linearity of matrix representation of linear transformation
Let V and W be finite-dimensional vector spaces with ordered bases β and γ, respectively, and let T, U: V→W be linear transformations. Then
- (a)
![[T+U]_\beta^\gamma=[T]_\beta^\gamma+[U]_\beta^\gamma](../I/m/17300a2dbc177e667040a5dbfedc49e0.png) and
and - (b)
![[aT]_\beta^\gamma=a[T]_\beta^\gamma](../I/m/357b101c089c43186a7014cd86f9afd9.png) for all scalars
for all scalars  .
.
 composition law of linear operators
composition law of linear operators
Let V,W, and Z be vector spaces over the same field f, and let T:V→W and U:W→Z be linear. then UT:V→Z is linear.
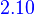 law of linear operator
law of linear operator
Let v be a vector space. Let T, U1, U2 ∈  (V). Then
(V). Then
(a) T(U1+U2)=TU1+TU2 and (U1+U2)T=U1T+U2T
(b) T(U1U2)=(TU1)U2
(c) TI=IT=T
(d)  (U1U2)=(
(U1U2)=( U1)U2=U1(
U1)U2=U1( U2) for all scalars
U2) for all scalars  .
.
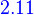 [UT]αγ=[U]βγ[T]αβ
[UT]αγ=[U]βγ[T]αβ
Let V, W and Z be finite-dimensional vector spaces with ordered bases α β γ, respectively. Let T: V→W and U: W→Z be linear transformations. Then
![[UT]_\alpha^\gamma=[U]_\beta^\gamma[T]_\alpha^\beta](../I/m/8aa29de8fcb3ea118faa0c7a84befc9e.png) .
.
Corollary. Let V be a finite-dimensional vector space with an ordered basis β. Let T,U∈ (V). Then [UT]β=[U]β[T]β.
(V). Then [UT]β=[U]β[T]β.
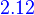 law of matrix
law of matrix
Let A be an m×n matrix, B and C be n×p matrices, and D and E be q×m matrices. Then
- (a) A(B+C)=AB+AC and (D+E)A=DA+EA.
- (b)
 (AB)=(
(AB)=( A)B=A(
A)B=A( B) for any scalar
B) for any scalar  .
. - (c) ImA=AIn.
- (d) If V is an n-dimensional vector space with an ordered basis β, then [Iv]β=In.
Corollary. Let A be an m×n matrix, B1,B2,...,Bk be n×p matrices, C1,C1,...,C1 be q×m matrices, and 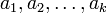 be scalars. Then
be scalars. Then
and
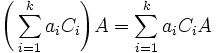 .
.
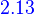 law of column multiplication
law of column multiplication
Let A be an m×n matrix and B be an n×p matrix. For each 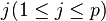 let
let 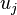 and
and  denote the jth columns of AB and B, respectively. Then
denote the jth columns of AB and B, respectively. Then
(a) 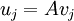
(b) 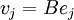 , where
, where  is the jth standard vector of Fp.
is the jth standard vector of Fp.
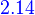 [T(u)]γ=[T]βγ[u]β
[T(u)]γ=[T]βγ[u]β
Let V and W be finite-dimensional vector spaces having ordered bases β and γ, respectively, and let T: V→W be linear. Then, for each u ∈ V, we have
![[T(u)]_\gamma=[T]_\beta^\gamma[u]_\beta](../I/m/ac694a8ea8dc6d246dcfcbc6bd1d436e.png) .
.
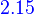 laws of LA
laws of LA
Let A be an m×n matrix with entries from F. Then the left-multiplication transformation LA: Fn→Fm is linear. Furthermore, if B is any other m×n matrix (with entries from F) and β and γ are the standard ordered bases for Fn and Fm, respectively, then we have the following properties.
(a) ![[L_A]_\beta^\gamma=A](../I/m/7a7c1ed454b8d3c7477f87be0f7b944b.png) .
.
(b) LA=LB if and only if A=B.
(c) LA+B=LA+LB and L A=
A= LA for all
LA for all  ∈F.
∈F.
(d) If T:Fn→Fm is linear, then there exists a unique m×n matrix C such that T=LC. In fact, ![\mathrm{C}=[L_T]_\beta^\gamma](../I/m/f26ba98f7f2349d70d05e6e151eb2982.png) .
.
(e) If W is an n×p matrix, then LAE=LALE.
(f ) If m=n, then 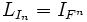 .
.
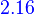 A(BC)=(AB)C
A(BC)=(AB)C
Let A,B, and C be matrices such that A(BC) is defined. Then A(BC)=(AB)C; that is, matrix multiplication is associative.
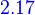 T−1is linear
T−1is linear
Let V and W be vector spaces, and let T:V→W be linear and invertible. Then T−1: W →V is linear.
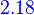 [T−1]γβ=([T]βγ)−1
[T−1]γβ=([T]βγ)−1
Let V and W be finite-dimensional vector spaces with ordered bases β and γ, respectively. Let T:V→W be linear. Then T is invertible if and only if ![[T]_\beta^\gamma](../I/m/6d85ed192e0de69832e36b12508e6681.png) is invertible. Furthermore,
is invertible. Furthermore, ![[T^{-1}]_\gamma^\beta=([T]_\beta^\gamma)^{-1}](../I/m/d62670e3b6f795ea86d9517cfaa7cf44.png)
Lemma. Let T be an invertible linear transformation from V to W. Then V is finite-dimensional if and only if W is finite-dimensional. In this case, dim(V)=dim(W).
Corollary 1. Let V be a finite-dimensional vector space with an ordered basis β, and let T:V→V be linear. Then T is invertible if and only if [T]β is invertible. Furthermore, [T−1]β=([T]β)−1.
Corollary 2. Let A be an n×n matrix. Then A is invertible if and only if LA is invertible. Furthermore, (LA)−1=LA−1.
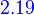 V is isomorphic to W ⇔ dim(V)=dim(W)
V is isomorphic to W ⇔ dim(V)=dim(W)
Let W and W be finite-dimensional vector spaces (over the same field). Then V is isomorphic to W if and only if dim(V)=dim(W).
Corollary. Let V be a vector space over F. Then V is isomorphic to Fn if and only if dim(V)=n.
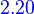 ??
??
Let V and W be finite-dimensional vector spaces over F of dimensions n and m, respectively, and let β and γ be ordered bases for V and W, respectively. Then the function 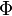 :
:  (V,W)→Mm×n(F), defined by
(V,W)→Mm×n(F), defined by ![~\Phi(T)=[T]_\beta^\gamma](../I/m/1f3b674e4d19ad3a2026d19462e2ebe9.png) for T∈
for T∈ (V,W), is an isomorphism.
(V,W), is an isomorphism.
Corollary. Let V and W be finite-dimensional vector spaces of dimension n and m, respectively. Then  (V,W) is finite-dimensional of dimension mn.
(V,W) is finite-dimensional of dimension mn.
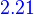 Φβ is an isomorphism
Φβ is an isomorphism
For any finite-dimensional vector space V with ordered basis β, Φβ is an isomorphism.
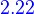 ??
??
Let β and β' be two ordered bases for a finite-dimensional vector space V, and let ![Q=[I_V]_{\beta'}^\beta](../I/m/d64664a7de2ef8d72c5b583a1da8480a.png) . Then
. Then
(a) 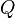 is invertible.
is invertible.
(b) For any 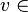 V,
V, ![~[v]_\beta=Q[v]_{\beta'}](../I/m/09083f4edd6bde5816abfb90ce1482c3.png) .
.
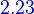 [T]β'=Q−1[T]βQ
[T]β'=Q−1[T]βQ
Let T be a linear operator on a finite-dimensional vector space V,and let β and β' be two ordered bases for V. Suppose that Q is the change of coordinate matrix that changes β'-coordinates into β-coordinates. Then
![~[T]_{\beta'}=Q^{-1}[T]_\beta Q](../I/m/fe32ee76fa44d6094873a89817556337.png) .
.
Corollary. Let A∈Mn×n(F), and le t γ be an ordered basis for Fn. Then [LA]γ=Q−1AQ, where Q is the n×n matrix whose jth column is the jth vector of γ.
Principal Axes Theorem
For a conic whose equation is 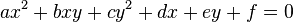 , the rotation given by
, the rotation given by 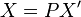 eliminates the
eliminates the  -term if
-term if  is an orthogonal matrix, with
is an orthogonal matrix, with 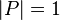 , that diagonalizes
, that diagonalizes  . That is,
. That is,
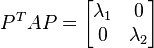 ,
,
where  and
and  are eigenvalues of
are eigenvalues of  . The equation of the rotated conic is given by
. The equation of the rotated conic is given by
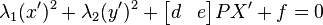 .
.
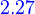 p(D)(x)=0 (p(D)∈C∞)⇒ x(k)exists (k∈N)
p(D)(x)=0 (p(D)∈C∞)⇒ x(k)exists (k∈N)
Any solution to a homogeneous linear differential equation with constant coefficients has derivatives of all orders; that is, if  is a solution to such an equation, then
is a solution to such an equation, then 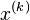 exists for every positive integer k.
exists for every positive integer k.
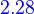 {solutions}= N(p(D))
{solutions}= N(p(D))
The set of all solutions to a homogeneous linear differential equation with constant coefficients coincides with the null space of p(D), where p(t) is the auxiliary polynomial with the equation.
Corollary. The set of all solutions to s homogeneous linear differential equation with constant coefficients is a subspace of 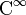 .
.
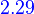 derivative of exponential function
derivative of exponential function
For any exponential function 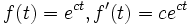 .
.
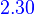 {e−at} is a basis of N(p(D+aI))
{e−at} is a basis of N(p(D+aI))
The solution space for the differential equation,
is of dimension 1 and has 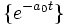 as a basis.
as a basis.
Corollary. For any complex number c, the null space of the differential operator D-cI has {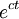 } as a basis.
} as a basis.
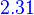
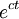 is a solution
is a solution
Let p(t) be the auxiliary polynomial for a homogeneous linear differential equation with constant coefficients. For any complex number c, if c is a zero of p(t), then to the differential equation.
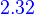 dim(N(p(D)))=n
dim(N(p(D)))=n
For any differential operator p(D) of order n, the null space of p(D) is an n_dimensional subspace of C∞.
Lemma 1. The differential operator D-cI: C∞ to C∞ is onto for any complex number c.
Lemma 2 Let V be a vector space, and suppose that T and U are linear operators on V such that U is onto and the null spaces of T and U are finite-dimensional, Then the null space of TU is finite-dimensional, and
- dim(N(TU))=dim(N(U))+dim(N(U)).
Corollary. The solution space of any nth-order homogeneous linear differential equation with constant coefficients is an n-dimensional subspace of C∞.
 ecit is linearly independent with each other (ci are distinct)
ecit is linearly independent with each other (ci are distinct)
Given n distinct complex numbers 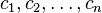 , the set of exponential functions
, the set of exponential functions 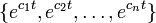 is linearly independent.
is linearly independent.
Corollary. For any nth-order homogeneous linear differential equation with constant coefficients, if the auxiliary polynomial has n distinct zeros 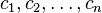 , then
, then 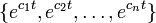 is a basis for the solution space of the differential equation.
is a basis for the solution space of the differential equation.
Lemma. For a given complex number c and positive integer n, suppose that (t-c)^n is athe auxiliary polynomial of a homogeneous linear differential equation with constant coefficients. Then the set
is a basis for the solution space of the equation.
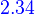 general solution of homogeneous linear differential equation
general solution of homogeneous linear differential equation
Given a homogeneous linear differential equation with constant coefficients and auxiliary polynomial
where 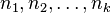 are positive integers and
are positive integers and 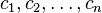 are distinct complex numbers, the following set is a basis for the solution space of the equation:
are distinct complex numbers, the following set is a basis for the solution space of the equation:
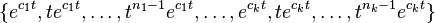 .
.
Definition of an Orthogonal Matrix
A square matrix  is called orthogonal if it is invertible and if
is called orthogonal if it is invertible and if
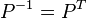 .
.
Real Spectral Theorem
If  is an
is an  symmetric matrix, then the following properties are true:
symmetric matrix, then the following properties are true:
-
 is diagonalizable.
is diagonalizable. - All eigenvalues of
 are real.
are real. - If
 is an eigenvalue of
is an eigenvalue of  with multiplicity
with multiplicity  , then
, then  has
has  linearly independent eigenvectors. That is, the eigenspace of
linearly independent eigenvectors. That is, the eigenspace of  has dimension
has dimension  .
.
Also, the set of eigenvalues of  is called the spectrum of
is called the spectrum of  .
.
Elementary matrix operations and systems of linear equations
Elementary matrix operations
The three elementary row operations are the following:
- Interchange two rows.
- Multiply a row by a nonzero constant.
- Add a multiple of a row to another row.
Elementary matrix
An  matrix is called an elementary matrix if it can be obtained from the identity matrix
matrix is called an elementary matrix if it can be obtained from the identity matrix  by a single elementary row operation.
by a single elementary row operation.
Rank of a matrix
The rank of a matrix A is the number of pivot columns after the reduced row echelon form of A.
Invertible Matrices
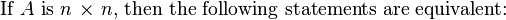
Determinants
If
is a 2×2 matrix with entries form a field F, then we define the determinant of A, denoted det(A) or |A|, to be the scalar  .
.
*Theorem 1: linear function for a single row.
*Theorem 2: nonzero determinant ⇔ invertible matrix
Theorem 1:
The function det: M2×2(F) → F is a linear function of each row of a 2×2 matrix when the other row is held fixed. That is, if 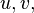 and
and  are in F² and
are in F² and  is a scalar, then
is a scalar, then
and
Theorem 2:
Let A  M2×2(F). Then thee deter minant of A is nonzero if and only if A is invertible. Moreover, if A is invertible, then
M2×2(F). Then thee deter minant of A is nonzero if and only if A is invertible. Moreover, if A is invertible, then
Diagonalization
Characteristic polynomial of a linear operator/matrix
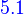 diagonalizable⇔basis of eigenvector
diagonalizable⇔basis of eigenvector
A linear operator T on a finite-dimensional vector space V is diagonalizable if and only if there exists an ordered basis β for V consisting of eigenvectors of T. Furthermore, if T is diagonalizable, 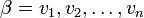 is an ordered basis of eigenvectors of T, and D = [T]β then D is a diagonal matrix and
is an ordered basis of eigenvectors of T, and D = [T]β then D is a diagonal matrix and 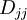 is the eigenvalue corresponding to
is the eigenvalue corresponding to  for
for  .
.
 eigenvalue⇔det(A-λIn)=0
eigenvalue⇔det(A-λIn)=0
Let A∈Mn×n(F). Then a scalar λ is an eigenvalue of A if and only if det(A-λIn)=0
 characteristic polynomial
characteristic polynomial
Let A∈Mn×n(F).
(a) The characteristic polynomial of A is a polynomial of degree n with leading coefficient (-1)n.
(b) A has at most n distinct eigenvalues.
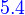 υ to λ⇔υ∈N(T-λI)
υ to λ⇔υ∈N(T-λI)
Let T be a linear operator on a vector space V, and let λ be an eigenvalue of T.
A vector υ∈V is an eigenvector of T corresponding to λ if and only if υ≠0 and υ∈N(T-λI).
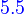 vi to λi⇔vi is linearly independent
vi to λi⇔vi is linearly independent
Let T be a linear operator on a vector space V, and let 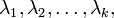 be distinct eigenvalues of T. If
be distinct eigenvalues of T. If 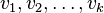 are eigenvectors of t such that
are eigenvectors of t such that  corresponds to
corresponds to  (
(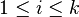 ), then {
), then {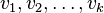 } is linearly independent.
} is linearly independent.
 characteristic polynomial splits
characteristic polynomial splits
The characteristic polynomial of any diagonalizable linear operator splits.
 1 ≤ dim(Eλ) ≤ m
1 ≤ dim(Eλ) ≤ m
Let T be alinear operator on a finite-dimensional vectorspace V, and let λ be an eigenvalue of T having multiplicity  . Then
. Then 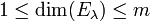 .
.
 S = S1 ∪ S2 ∪ ...∪ Sk is linearly independent
S = S1 ∪ S2 ∪ ...∪ Sk is linearly independent
Let T be a linear operator on a vector space V, and let 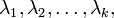 be distinct eigenvalues of T. For each
be distinct eigenvalues of T. For each 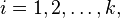 let
let 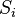 be a finite linearly independent subset of the eigenspace
be a finite linearly independent subset of the eigenspace 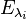 . Then
. Then 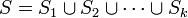 is a linearly independent subset of V.
is a linearly independent subset of V.
 ⇔T is diagonalizable
⇔T is diagonalizable
Let T be a linear operator on a finite-dimensional vector space V that the characteristic polynomial of T splits. Let 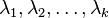 be the distinct eigenvalues of T. Then
be the distinct eigenvalues of T. Then
(a) T is diagonalizable if and only if the multiplicity of  is equal to
is equal to 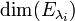 for all
for all  .
.
(b) If T is diagonalizable and  is an ordered basis for
is an ordered basis for 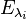 for each
for each  , then
, then 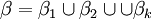 is an ordered
is an ordered 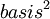 for V consisting of eigenvectors of T.
for V consisting of eigenvectors of T.
Test for diagonlization
Inner product spaces
Inner product, standard inner product on Fn, conjugate transpose, adjoint, Frobenius inner product, complex/real inner product space, norm, length, conjugate linear, orthogonal, perpendicular, unit vector, orthonormal, normalization.
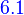 properties of linear product
properties of linear product
Let V be an inner product space. Then for x,y,z ∈ V and c ∈ F, the following statements are true.
(a) 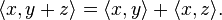
(b) 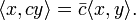
(c) 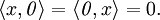
(d) 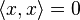 if and only if
if and only if 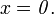
(e) If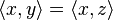 for all
for all 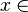 V, then
V, then  .
.
 law of norm
law of norm
Let V be an inner product space over F. Then for all x,y ∈ V and c ∈ F, the following statements are true.
(a) 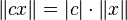 .
.
(b)  if and only if
if and only if 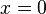 . In any case,
. In any case,  .
.
(c)(Cauchy-Schwarz Inequality)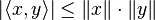 .
.
(d)(Triangle Inequality)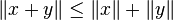 .
.
orthonormal basis, Gram–Schmidt process, Fourier coefficients, orthogonal complement, orthogonal projection
 span of orthogonal subset
span of orthogonal subset
Let V be an inner product space and 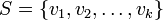 be an orthogonal subset of V consisting of nonzero vectors. If
be an orthogonal subset of V consisting of nonzero vectors. If 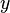 ∈span(S), then
∈span(S), then
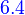 Gram-Schmidt process
Gram-Schmidt process
Let V be an inner product space and S=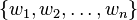 be a linearly independent subset of V. DefineS'=
be a linearly independent subset of V. DefineS'=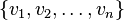 , where
, where  and
and
Then S' is an orhtogonal set of nonzero vectors such that span(S')=span(S).
 orthonormal basis
orthonormal basis
Let V be a nonzero finite-dimensional inner product space. Then V has an orthonormal basis β. Furthermore, if β =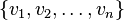 and x∈V, then
and x∈V, then
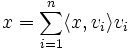 .
.
Corollary. Let V be a finite-dimensional inner product space with an orthonormal basis β =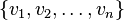 . Let T be a linear operator on V, and let A=[T]β. Then for any
. Let T be a linear operator on V, and let A=[T]β. Then for any  and
and 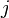 ,
, 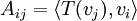 .
.
 W⊥ by orthonormal basis
W⊥ by orthonormal basis
Let W be a finite-dimensional subspace of an inner product space V, and let 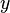 ∈V. Then there exist unique vectors
∈V. Then there exist unique vectors 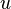 ∈W and
∈W and 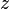 ∈W⊥ such that
∈W⊥ such that 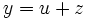 . Furthermore, if
. Furthermore, if 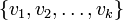 is an orthornormal basis for W, then
is an orthornormal basis for W, then
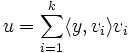 .
.
S=\{v_1,v_2,\ldots,v_k\}
Corollary. In the notation of Theorem 6.6, the vector 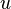 is the unique vector in W that is "closest" to
is the unique vector in W that is "closest" to 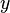 ; thet is, for any
; thet is, for any  ∈W,
∈W, 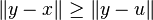 , and this inequality is an equality if and onlly if
, and this inequality is an equality if and onlly if 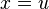 .
.
 properties of orthonormal set
properties of orthonormal set
Suppose that 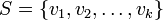 is an orthonormal set in an
is an orthonormal set in an  -dimensional inner product space V. Than
-dimensional inner product space V. Than
(a) S can be extended to an orthonormal basis 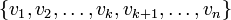 for V.
for V.
(b) If W=span(S), then 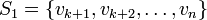 is an orhtonormal basis for W⊥(using the preceding notation).
is an orhtonormal basis for W⊥(using the preceding notation).
(c) If W is any subspace of V, then dim(V)=dim(W)+dim(W⊥).
Least squares approximation, Minimal solutions to systems of linear equations
 linear functional representation inner product
linear functional representation inner product
Let V be a finite-dimensional inner product space over F, and let  :V→F be a linear transformation. Then there exists a unique vector
:V→F be a linear transformation. Then there exists a unique vector 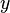 ∈ V such that
∈ V such that 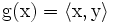 for all
for all  ∈ V.
∈ V.
 definition of T*
definition of T*
Let V be a finite-dimensional inner product space, and let T be a linear operator on V. Then there exists a unique function T*:V→V such that 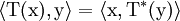 for all
for all  ∈ V. Furthermore, T* is linear
∈ V. Furthermore, T* is linear
 [T*]β=[T]*β
[T*]β=[T]*β
Let V be a finite-dimensional inner product space, and let β be an orthonormal basis for V. If T is a linear operator on V, then
![[T^*]_\beta=[T]^*_\beta](../I/m/681ff785b59e25c8ec321f56acfe2767.png) .
.
 properties of T*
properties of T*
Let V be an inner product space, and let T and U be linear operators onV. Then
(a) (T+U)*=T*+U*;
(b) ( T)*=
T)*=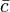 T* for any c∈ F;
T* for any c∈ F;
(c) (TU)*=U*T*;
(d) T**=T;
(e) I*=I.
Corollary. Let A and B be n×nmatrices. Then
(a) (A+B)*=A*+B*;
(b) ( A)*=
A)*=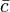 A* for any
A* for any  ∈ F;
∈ F;
(c) (AB)*=B*A*;
(d) A**=A;
(e) I*=I.
 Least squares approximation
Least squares approximation
Let A ∈ Mm×n(F) and 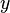 ∈Fm. Then there exists
∈Fm. Then there exists 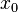 ∈ Fn such that
∈ Fn such that 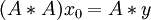 and
and 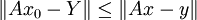 for all x∈ Fn
for all x∈ Fn
Lemma 1. let A ∈ Mm×n(F),  ∈Fn, and
∈Fn, and  ∈Fm. Then
∈Fm. Then
Lemma 2. Let A ∈ Mm×n(F). Then rank(A*A)=rank(A).
Corollary.(of lemma 2) If A is an m×n matrix such that rank(A)=n, then A*A is invertible.
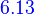 Minimal solutions to systems of linear equations
Minimal solutions to systems of linear equations
Let A ∈ Mm×n(F) and b∈ Fm. Suppose that  is consistent. Then the following statements are true.
is consistent. Then the following statements are true.
(a) There existes exactly one minimal solution  of
of  , and
, and  ∈R(LA*).
∈R(LA*).
(b) The vector  is the only solution to
is the only solution to  that lies in R(LA*); that is, if
that lies in R(LA*); that is, if 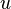 satisfies
satisfies 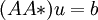 , then
, then 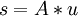 .
.
References
- Linear Algebra 4th edition, by Stephen H. Friedberg Arnold J. Insel and Lawrence E. spence ISBN 7-04-016733-6
- Linear Algebra 3rd edition, by Serge Lang (UTM) ISBN 0-387-96412-6
- Linear Algebra and Its Applications 4th edition, by Gilbert Strang ISBN 0-03-010567-6