Tetrakis hexahedron
| Tetrakis hexahedron | |
|---|---|
 (Click here for rotating model) | |
| Type | Catalan solid |
| Coxeter diagram | |
| Conway notation | kC |
| Face type | V4.6.6 isosceles triangle |
| Faces | 24 |
| Edges | 36 |
| Vertices | 14 |
| Vertices by type | 6{4}+8{6} |
| Symmetry group | Oh, B3, [4,3], (*432) |
| Rotation group | O, [4,3]+, (432) |
| Dihedral angle | 143° 7' 48"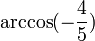 |
| Properties | convex, face-transitive |
 Truncated octahedron (dual polyhedron) |
 Net |
In geometry, a tetrakis hexahedron (also known as a tetrahexahedron, hextetrahedron and kiscube[1]) is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
It also can be called a disdyakis hexahedron as the dual of an omnitruncated tetrahedron.
Orthogonal projections
The tetrakis hexahedron, dual of the truncated octahedron has 3 symmetry positions, two located on vertices and one mid-edge.
| Projective symmetry |
[2] | [4] | [6] |
|---|---|---|---|
| Tetrakis hexahedron |
 |
 |
 |
| Truncated octahedron |
 |
 |
 |
Uses
Naturally occurring (crystal) formations of tetrahexahedra are observed in copper and fluorite systems.
Polyhedral dice shaped like the tetrakis hexahedron are occasionally used by gamers.
A 24-cell viewed under a vertex-first perspective projection has a surface topology of a tetrakis hexahedron and the geometric proportions of the rhombic dodecahedron, with the rhombic faces divided into two triangles.
The tetrakis hexahedron appears as one of the simplest examples in building theory. Consider the Riemannian symmetric space associated to the group SL4(R). Its Tits boundary has the structure of a spherical building whose apartments are 2-dimensional spheres. The partition of this sphere into spherical simplices (chambers) can be obtained by taking the radial projection of a tetrakis hexahedron.
Symmetry
With Td, [3,3] (*332) tetrahedral symmetry, the triangular faces represent the 24 fundamental domains of tetrahdral symmetry. This polyhedron can be constructed from 6 great circles on a sphere. It can also be seen by a cube with its square faces triangulated by their vertices and face centers and a tetrahedron with its faces divided by vertices, mid-edges, and a central point.
 |
 |
 |
 |
The edges of the tetrakis hexahedron form 6 circles (or centrally radial lines) in the plane. Each of these 6 circles represent a mirror line in tetrahedral symmetry. The 6 circles can be grouped into 3 sets of 2 pairs of orthogonal circles. These edges can also be seen as a compound of 3 othogonal square hosohedrons.
| stereographic projection | Perspective | |||
|---|---|---|---|---|
 |
 |
 |
 |
 |
| [4] | [3] | [2] | Skew | |
Dimensions
If we denote the edge length of the base cube by a,
the height of each pyramid summit above the cube is a/4.
The inclination of each triangular face of the pyramid versus the cube face
is arctan(1/2), approximately 26.565 degrees (sequence A073000 in OEIS).
One edge of the isosceles triangles has length a, the other two have
length 3a/4, which follows by applying the Pythagorean theorem to height and base length. This yields an altitude of √5 a/4 in the triangle (![]() A204188). Its area is √5a/8, and the internal angles are arccos(2/3) (approximately 48.1897 degrees) and the complementary 180-2arccos(2/3) (approximately 83.6206 degrees).
A204188). Its area is √5a/8, and the internal angles are arccos(2/3) (approximately 48.1897 degrees) and the complementary 180-2arccos(2/3) (approximately 83.6206 degrees).
The volume of the pyramid is a3/12; so the total volume of the six pyramids and the cube in the hexahedron is 3a3/2.
Kleetope
It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.
Cubic pyramid
It is very similar to the net for a Cubic pyramid, as the net for a square based is a square with triangles attached to each edge, the net for a cubic pyramid is a cube with square pyramids attached to each face.
Related polyhedra and tilings

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sym. *n42 [n,3] |
Spherical | Euclid. | Compact hyperb. | Parac. | Noncompact hyperbolic | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | ||
| Truncated figures |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Config. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| n-kis figures |
 |
 |
 |
 |
 |
 |
 |
|||||
| Config. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
It is a polyhedra in a sequence defined by the face configuration V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any 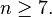
With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group with order 2,3,n mirrors at each triangle face vertex.
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Figures |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
See also
References
- ↑ Conway, Symmetries of things, p.284
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 730208 (The thirteen semiregular convex polyhedra and their duals, Page 14, Tetrakishexahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Tetrakis hexahedron)
External links
- Eric W. Weisstein, Tetrakis hexahedron (Catalan solid) at MathWorld
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
- VRML model
- Conway Notation for Polyhedra Try: "dtO" or "kC"
- Tetrakis Hexahedron – Interactive Polyhedron model
- The Uniform Polyhedra
| ||||||||||||||||||||||||||||||||||||
