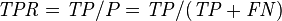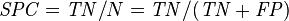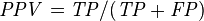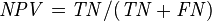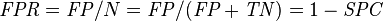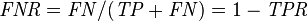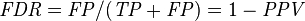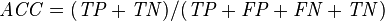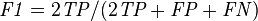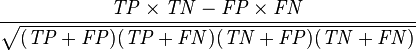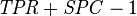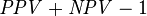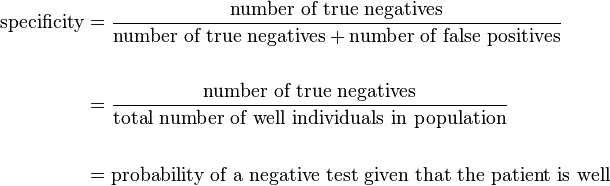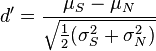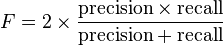Sensitivity and specificity
Sensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function:
- Sensitivity (also called the true positive rate, or the recall in some fields) measures the proportion of positives that are correctly identified as such (e.g., the percentage of sick people who are correctly identified as having the condition).
- Specificity (also called the true negative rate) measures the proportion of negatives that are correctly identified as such (e.g., the percentage of healthy people who are correctly identified as not having the condition).
Thus sensitivity quantifies the avoiding of false negatives, as specificity does for false positives.
For any test, there is usually a trade-off between the measures. For instance, in an airport security setting in which one is testing for potential threats to safety, scanners may be set to trigger on low-risk items like belt buckles and keys (low specificity), in order to reduce the risk of missing objects that do pose a threat to the aircraft and those aboard (high sensitivity). This trade-off can be represented graphically as a receiver operating characteristic curve.
A perfect predictor would be described as 100% sensitive (e.g., all sick are identified as sick) and 100% specific (e.g., no healthy are identified as sick); however, theoretically any predictor will possess a minimum error bound known as the Bayes error rate.
Definitions
|
Imagine a study evaluating a new test that screens people for a disease. Each person taking the test either has or does not have the disease. The test outcome can be positive (classifying the person as having the disease) or negative (classifying the person as not having the disease). The test results for each subject may or may not match the subject's actual status. In that setting:
- True positive: Sick people correctly identified as sick
- False positive: Healthy people incorrectly identified as sick
- True negative: Healthy people correctly identified as healthy
- False negative: Sick people incorrectly identified as healthy
In general, Positive = identified and negative = rejected. Therefore:
- True positive = correctly identified
- False positive = incorrectly identified
- True negative = correctly rejected
- False negative = incorrectly rejected
Let us consider a group with P positive instances and N negative instances of some condition. The four outcomes can be formulated in a 2×2 contingency table or confusion matrix, as follows:
| True condition | |||||
| Total population | Condition positive | Condition negative | Prevalence = Σ Condition positive/Σ Total population | ||
| Predicted condition |
Predicted condition positive |
True positive | False positive (Type I error) |
Positive predictive value (PPV), Precision = Σ True positive/Σ Test outcome positive | False discovery rate (FDR) = Σ False positive/Σ Test outcome positive |
| Predicted condition negative |
False negative (Type II error) |
True negative | False omission rate (FOR) = Σ False negative/Σ Test outcome negative | Negative predictive value (NPV) = Σ True negative/Σ Test outcome negative | |
| Accuracy (ACC) = Σ True positive + Σ True negative/Σ Total population | True positive rate (TPR), Sensitivity, Recall = Σ True positive/Σ Condition positive | False positive rate (FPR), Fall-out = Σ False positive/Σ Condition negative | Positive likelihood ratio (LR+) = TPR/FPR | Diagnostic odds ratio (DOR) = LR+/LR− | |
| False negative rate (FNR), Miss rate = Σ False negative/Σ Condition positive | True negative rate (TNR), Specificity (SPC) = Σ True negative/Σ Condition negative | Negative likelihood ratio (LR−) = FNR/TNR | |||
Sensitivity
Sensitivity refers to the test's ability to correctly detect patients who do have the condition. Consider the example of a medical test used to identify a disease. The sensitivity of the test is the proportion of people who test positive for the disease among those who have the disease. Mathematically, this can be expressed as:
A negative result in a test with high sensitivity is useful for ruling out disease. A high sensitivity test is reliable when its result is negative, since it rarely misdiagnoses those who have the disease. A test with 100% sensitivity will recognize all patients with the disease by testing positive. A negative test result would definitively rule out presence of the disease in a patient.
A positive result in a test with high sensitivity is not useful for ruling in disease. Suppose a 'bogus' test kit is designed to show only one reading, positive. When used on diseased patients, all patients test positive, giving the test 100% sensitivity. However, sensitivity by definition does not take into account false positives. The bogus test also returns positive on all healthy patients, giving it a false positive rate of 100%, rendering it useless for detecting or "ruling in" the disease.
Sensitivity is not the same as the precision or positive predictive value (ratio of true positives to combined true and false positives), which is as much a statement about the proportion of actual positives in the population being tested as it is about the test.
The calculation of sensitivity does not take into account indeterminate test results. If a test cannot be repeated, indeterminate samples either should be excluded from the analysis (the number of exclusions should be stated when quoting sensitivity) or can be treated as false negatives (which gives the worst-case value for sensitivity and may therefore underestimate it).
A test with high sensitivity has a low type II error rate. In non-medical contexts, sensitivity is sometimes called recall.
Specificity
Specificity relates to the test's ability to correctly detect patients without a condition. Consider the example of a medical test for diagnosing a disease. Specificity of a test is the proportion of healthy patients known not to have the disease, who will test negative for it. Mathematically, this can also be written as:
A positive result in a test with high specificity is useful for ruling in disease. The test rarely gives positive results in healthy patients. A test with 100% specificity will read negative, and accurately exclude disease from all healthy patients. A positive result signifies a high probability of the presence of disease.[3]
A negative result in a test with high specificity is not useful for ruling out disease. Assume a 'bogus' test is designed to read only negative. This is administered to healthy patients, and reads negative on all of them. This will give the test a specificity of 100%. Specificity by definition does not take into account false negatives. The same test will also read negative on diseased patients, therefore it has a false negative rate of 100%, and will be useless for ruling out disease.
A test with a high specificity has a low type I error rate.
Graphical illustration
-

High sensitivity and low specificity
-

Low sensitivity and high specificity
Medical examples
In medical diagnosis, test sensitivity is the ability of a test to correctly identify those with the disease (true positive rate), whereas test specificity is the ability of the test to correctly identify those without the disease (true negative rate). If 100 patients known to have a disease were tested, and 43 test positive, then the test has 43% sensitivity. If 100 with no disease are tested and 96 return a negative result, then the test has 96% specificity. Sensitivity and specificity are prevalence-independent test characteristics, as their values are intrinsic to the test and do not depend on the disease prevalence in the population of interest.[4] Positive and negative predictive values, but not sensitivity or specificity, are values influenced by the prevalence of disease in the population that is being tested. These concepts are illustrated graphically in this applet Bayesian clinical diagnostic model which show the positive and negative predictive values as a function of the prevalence, the sensitivity and specificity.
Misconceptions
It is often claimed that a highly specific test is effective at ruling in a disease when positive, while a highly sensitive test is deemed effective at ruling out a disease when negative.[5][6] This has led to the widely used mnemonics SPIN and SNOUT, according to which a highly SPecific test, when Positive, rules IN disease (SP-P-IN), and a highly 'SeNsitive' test, when Negative rules OUT disease (SN-N-OUT). Both rules of thumb are, however, inferentially misleading, as the diagnostic power of any test is determined by both its sensitivity and its specificity.[7][8][9]
The tradeoff between Specificity and Sensitivity is explored in ROC analysis as a trade off between TPR and FPR (that is Recall and Fallout).[1] Giving them equal weight optimizes Informedness = Specificity+Sensitivity-1 = TPR-FPR, the magnitude of which gives the probability of an informed decision between the two classes (>0 represents appropriate use of information, 0 represents chance-level performance, <0 represents perverse use of information).[2]
Sensitivity index
The sensitivity index or d' (pronounced 'dee-prime') is a statistic used in signal detection theory. It provides the separation between the means of the signal and the noise distributions, compared against the standard deviation of the noise distribution. For normally distributed signal and noise with mean and standard deviations 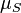 and
and 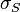 , and
, and 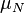 and
and 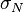 , respectively, d' is defined as:
, respectively, d' is defined as:
An estimate of d' can be also found from measurements of the hit rate and false-alarm rate. It is calculated as:
- d' = Z(hit rate) - Z(false alarm rate),[11]
where function Z(p), p ∈ [0,1], is the inverse of the cumulative Gaussian distribution.
d' is a dimensionless statistic. A higher d' indicates that the signal can be more readily detected.
Worked example
- A worked example
- A diagnostic test with sensitivity 67% and specificity 91% is applied to 2030 people to look for a disorder with a population prevalence of 1.48%
| Patients with bowel cancer (as confirmed on endoscopy) | ||||
| Condition positive | Condition negative | |||
| Fecal occult blood screen test outcome |
Test outcome positive |
True positive (TP) = 20 |
False positive (FP) = 180 |
Positive predictive value = TP / (TP + FP) = 20 / (20 + 180) = 10% |
| Test outcome negative |
False negative (FN) = 10 |
True negative (TN) = 1820 |
Negative predictive value = TN / (FN + TN) = 1820 / (10 + 1820) ≈ 99.5% | |
| Sensitivity = TP / (TP + FN) = 20 / (20 + 10) ≈ 67% |
Specificity = TN / (FP + TN) = 1820 / (180 + 1820) = 91% | |||
Related calculations
- False positive rate (α) = type I error = 1 − specificity = FP / (FP + TN) = 180 / (180 + 1820) = 9%
- False negative rate (β) = type II error = 1 − sensitivity = FN / (TP + FN) = 10 / (20 + 10) = 33%
- Power = sensitivity = 1 − β
- Likelihood ratio positive = sensitivity / (1 − specificity) = 0.67 / (1 − 0.91) = 7.4
- Likelihood ratio negative = (1 − sensitivity) / specificity = (1 − 0.67) / 0.91 = 0.37
Hence with large numbers of false positives and few false negatives, a positive screen test is in itself poor at confirming the disorder (PPV = 10%) and further investigations must be undertaken; it did, however, correctly identify 66.7% of all cases (the sensitivity). However as a screening test, a negative result is very good at reassuring that a patient does not have the disorder (NPV = 99.5%) and at this initial screen correctly identifies 91% of those who do not have cancer (the specificity).
Estimation of errors in quoted sensitivity or specificity
Sensitivity and specificity values alone may be highly misleading. The 'worst-case' sensitivity or specificity must be calculated in order to avoid reliance on experiments with few results. For example, a particular test may easily show 100% sensitivity if tested against the gold standard four times, but a single additional test against the gold standard that gave a poor result would imply a sensitivity of only 80%. A common way to do this is to state the binomial proportion confidence interval, often calculated using a Wilson score interval.
Confidence intervals for sensitivity and specificity can be calculated, giving the range of values within which the correct value lies at a given confidence level (e.g., 95%).[12]
Terminology in information retrieval
In information retrieval, the positive predictive value is called precision, and sensitivity is called recall. Unlike the Specificity vs Sensitivity tradeoff, these measures are both independent of the number of true negatives, which is generally unknown and much larger than the actual numbers of relevant and retrieved documents. This assumption of very large numbers of true negatives versus positives is rare in other applications.[2]
The F-score can be used as a single measure of performance of the test for the positive class. The F-score is the harmonic mean of precision and recall:
In the traditional language of statistical hypothesis testing, the sensitivity of a test is called the statistical power of the test, although the word power in that context has a more general usage that is not applicable in the present context. A sensitive test will have fewer Type II errors.
See also
- Accuracy and precision
- Brier score
- NCSS (statistical software) includes sensitivity and specificity analysis.
- OpenEpi software program
- Discrimination
- Statistical significance
- Uncertainty coefficient, aka Proficiency
- Youden's J statistic
References
- 1 2 Fawcett, Tom (2006). "An Introduction to ROC Analysis". Pattern Recognition Letters 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- 1 2 3 Powers, David M W (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation" (PDF). Journal of Machine Learning Technologies 2 (1): 37–63.
- ↑ "SpPins and SnNouts". Centre for Evidence Based Medicine (CEBM). Retrieved 26 December 2013.
- ↑ Mangrulkar, Rajesh. "Diagnostic Reasoning I and II". Retrieved 24 January 2012.
- ↑ "Evidence-Based Diagnosis". Michigan State University.
- ↑ "Sensitivity and Specificity". Emory University Medical School Evidence Based Medicine course.
- ↑ Baron, JA (Apr–Jun 1994). "Too bad it isn't true.....". Medical decision making : an international journal of the Society for Medical Decision Making 14 (2): 107. doi:10.1177/0272989X9401400202. PMID 8028462.
- ↑ Boyko, EJ (Apr–Jun 1994). "Ruling out or ruling in disease with the most sensitive or specific diagnostic test: short cut or wrong turn?". Medical decision making : an international journal of the Society for Medical Decision Making 14 (2): 175–179. doi:10.1177/0272989X9401400210. PMID 8028470.
- ↑ Pewsner, D; Battaglia, M; Minder, C; Marx, A; Bucher, HC; Egger, M (Jul 24, 2004). "Ruling a diagnosis in or out with "SpPIn" and "SnNOut": a note of caution". BMJ (Clinical research ed.) 329 (7459): 209–13. doi:10.1136/bmj.329.7459.209. PMC 487735. PMID 15271832.
- ↑ Gale, SD; Perkel, DJ (Jan 20, 2010). "A basal ganglia pathway drives selective auditory responses in songbird dopaminergic neurons via disinhibition". The Journal of neuroscience : the official journal of the Society for Neuroscience 30 (3): 1027–1037. doi:10.1523/JNEUROSCI.3585-09.2010. PMC 2824341. PMID 20089911.
- ↑ Macmillan, Neil A.; Creelman, C. Douglas (15 September 2004). Detection Theory: A User's Guide. Psychology Press. p. 7. ISBN 978-1-4106-1114-7.
- ↑ "Diagnostic test online calculator calculates sensitivity, specificity, likelihood ratios and predictive values from a 2x2 table - calculator of confidence intervals for predictive parameters". medcalc.org.
Further reading
- Altman DG, Bland JM (1994). "Diagnostic tests. 1: Sensitivity and specificity". BMJ 308 (6943): 1552. doi:10.1136/bmj.308.6943.1552. PMC 2540489. PMID 8019315.
- Loong T (2003). "Understanding sensitivity and specificity with the right side of the brain". BMJ 327 (7417): 716–719. doi:10.1136/bmj.327.7417.716. PMC 200804. PMID 14512479.
External links
- UIC Calculator
- Vassar College's Sensitivity/Specificity Calculator
- MedCalc Free Online Calculator
- Bayesian clinical diagnostic model applet
| ||||||||||||||||||||||||||||||||||