Terminal and nonterminal symbols

In computer science, terminal and nonterminal symbols are the lexical elements used in specifying the production rules constituting a formal grammar. Terminal symbols are the elementary symbols of the language defined by a formal grammar. Nonterminal symbols (or syntactic variables) are replaced by groups of terminal symbols according to the production rules.

The terminals and nonterminals of a particular grammar are two disjoint sets.

Terminal symbols

Terminal symbols are literal symbols which may appear in the outputs of the production rules of a formal grammar and which cannot be changed using the rules of the grammar (this is the reason for the name "terminal").

For concreteness, consider a grammar defined by two rules. We will use no English symbols. Using symbols that don't belong to the English alphabet, you will forget the concept of "word" reading the sentences and you get focus in pictoric marks interacting each other:

The symbol ר can become ди
The symbol ר can become д

Here д is a terminal symbol because no rule exists which would change it into something else. (On the other hand, ר has two rules that can change it, thus it is nonterminal.) A formal language defined (or generated) by a particular grammar is the set of strings that can be produced by the grammar and that consist only of terminal symbols.

Nonterminal symbols

Nonterminal symbols are those symbols which can be replaced. They may also be called simply syntactic variables. A formal grammar includes a start symbol, a designated member of the set of nonterminals from which all the strings in the language may be derived by successive applications of the production rules. In fact, the language defined by a grammar is precisely the set of terminal strings that can be so derived.

Context-free grammars are those grammars in which the left-hand side of each production rule consists of only a single nonterminal symbol. This restriction is non-trivial; not all languages can be generated by context-free grammars. Those that can are called context-free languages. These are exactly the languages that can be recognized by a non-deterministic push down automaton. Context-free languages are the theoretical basis for the syntax of most programming languages.

Production rules

A grammar is defined by production rules (or just 'productions') that specify which symbols may replace which other symbols; these rules may be used to generate strings, or to parse them. Each such rule has a head, or left-hand side, which consists of the string that may be replaced, and a body, or right-hand side, which consists of a string that may replace it. Rules are often written in the form head → body; e.g., the rule a → b specifies that a can be replaced by b.

In the classic formalization of generative grammars first proposed by Noam Chomsky in the 1950s,^[1]^[2] a grammar G consists of the following components:

A finite set $N$ of nonterminal symbols.
A finite set 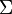$\Sigma$ of terminal symbols that is disjoint from $N$ .
A finite set $P$ of production rules, each rule of the form

(\Sigma \cup N)^{*} N (\Sigma \cup N)^{*} \rightarrow (\Sigma \cup N)^{*}

where

{}^{*}

is the Kleene star operator and

\cup

denotes set union, so

(\Sigma \cup N)^{*}

represents zero or more symbols, and

N

means one nonterminal symbol. That is, each production rule maps from one string of symbols to another, where the first string contains at least one nonterminal symbol. In the case that the body consists solely of the empty string—i.e., that it contains no symbols at all—it may be denoted with a special notation (often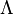

\Lambda

e

\epsilon

) in order to avoid confusion.

A distinguished symbol $S \in N$ that is the start symbol.

A grammar is formally defined as the ordered quadruple 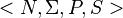$<N, \Sigma, P, S>$ . Such a formal grammar is often called a rewriting system or a phrase structure grammar in the literature.^[3]^[4]

Example

For instance, the following represents an integer (which may be signed) expressed in a variant of Backus–Naur form:

<digit> ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'
<integer> ::= ['-'] <digit> {<digit>}

In this example, the symbols (-,0,1,2,3,4,5,6,7,8,9) are terminal symbols and <digit> and <integer> are nonterminal symbols.

Note: Strings with leading zeroes like "0056" or "0000" will be also in that language.

References

↑ Chomsky, Noam (1956). "Three Models for the Description of Language". IRE Transactions on Information Theory 2 (2): 113–123. doi:10.1109/TIT.1956.1056813.
↑ Chomsky, Noam (1957). Syntactic Structures. The Hague: Mouton.
↑ Ginsburg, Seymour (1975). Algebraic and automata theoretic properties of formal languages. North-Holland. pp. 8–9. ISBN 0-7204-2506-9.
↑ Harrison, Michael A. (1978). Introduction to Formal Language Theory. Reading, Mass.: Addison-Wesley Publishing Company. p. 13. ISBN 0-201-02955-3.

This article is issued from Wikipedia - version of the Monday, November 09, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.