Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras.[1]
Definition
Let R be a commutative ring and let A and B be R-algebras. Since A and B may both be regarded as R-modules, we may form their tensor product
which is also an R-module. We can give the tensor product the structure of an algebra by defining the product on elements of the form a ⊗ b by[2][3]
and then extending by linearity to all of A ⊗R B. This product is R-bilinear, associative, and unital with an identity element given by 1A ⊗ 1B,[4] where 1A and 1B are the identities of A and B. If A and B are both commutative then the tensor product is commutative as well.
The tensor product turns the category of all R-algebras into a symmetric monoidal category.
Further properties
There are natural homomorphisms of A and B to A ⊗R B given by[5]
These maps make the tensor product a coproduct in the category of commutative R-algebras. The tensor product is not the coproduct in the category of all R-algebras. There the coproduct is given by a more general free product of algebras. Nevertheless the tensor product of non-commutative algebras can be described by an universal property similar to that of the coproduct:
The natural isomorphism is given by identifying a morphism 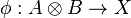 on the left hand side with the pair of morphism
on the left hand side with the pair of morphism  on the right hand side where
on the right hand side where 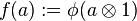 and similarly
and similarly 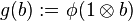 .
.
Applications
The tensor product of algebras is of constant use in algebraic geometry: working in the opposite category to that of commutative R-algebras, it provides pullbacks of affine schemes, otherwise known as fiber products.
See also
- Extension of scalars
- Tensor product of modules
- Tensor product of fields
- Linearly disjoint
- Multilinear subspace learning
Notes
References
- Kassel, Christian (1995), Quantum groups, Graduate texts in mathematics 155, Springer, ISBN 978-0-387-94370-1.
- Lang, Serge (2002) [first published in 1993]. Algebra. Graduate Texts in Mathematics 21. Springer. ISBN 0-387-95385-X.
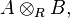

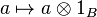

![Hom(A\otimes B,X)\cong \lbrace (f,g)\in Hom(A,X)\times Hom(B,X)\mid \forall a\in A,b\in B:[f(a),g(b)]=0\rbrace](../I/m/103b91bfbd7b9a3ad247d5b09ee35201.png)