Tarski monster group

This article is about the kind of infinite group known as a Tarski monster group. For the largest of the sporadic simple groups, see Monster group.

In the area of modern algebra known as group theory, a Tarski monster group, named for Alfred Tarski, is an infinite group G, such that every proper subgroup H of G, other than the identity subgroup, is a cyclic group of order a fixed prime number p. A Tarski monster group is necessarily simple. It was shown by A. Yu. Olshanskii in 1979 that Tarski groups exist, and that there is a Tarski p-group for every prime p > 10⁷⁵. They are a source of counterexamples to conjectures in group theory, most importantly to Burnside's problem and the von Neumann conjecture.

Definition

Let $p$ be a fixed prime number. An infinite group $G$ is called a Tarski Monster group for $p$ if every nontrivial subgroup (i.e. every subgroup other than 1 and G itself) has $p$ elements.

Properties

$G$ is necessarily finitely generated. In fact it is generated by every two non-commuting elements.
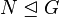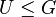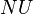$G$ is simple. If $N\trianglelefteq G$ and $U\leq G$ is any subgroup distinct from $N$ the subgroup $NU$ would have $p^2$ elements.
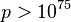The construction of Ol'shanskii shows in fact that there are continuum-many non-isomorphic Tarski Monster groups for each prime $p>10^{75}$ .

References

A. Yu. Olshanskii, An infinite group with subgroups of prime orders, Math. USSR Izv. 16 (1981), 279–289; translation of Izvestia Akad. Nauk SSSR Ser. Matem. 44 (1980), 309–321.
A. Yu. Olshanskii, Groups of bounded period with subgroups of prime order, Algebra and Logic 21 (1983), 369–418; translation of Algebra i Logika 21 (1982), 553–618.
Ol'shanskiĭ, A. Yu. (1991), Geometry of defining relations in groups, Mathematics and its Applications (Soviet Series) 70, Dordrecht: Kluwer Academic Publishers Group, ISBN 978-0-7923-1394-6

This article is issued from Wikipedia - version of the Thursday, April 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.