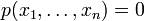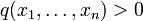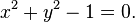Tarski–Seidenberg theorem

In mathematics, the Tarski–Seidenberg theorem states that a set in (n + 1)-dimensional space defined by polynomial equations and inequalities can be projected down onto n-dimensional space, and the resulting set is still definable in terms of polynomial identities and inequalities. The theorem — also known as the Tarski–Seidenberg projection property — is named after Alfred Tarski and Abraham Seidenberg. It implies that quantifier elimination is possible over the reals, that is that every formula constructed from polynomial equations and inequalities by logical connectors ∨ (or), ∧ (and), ¬ (not) and quantifiers ∀ (for all), ∃ (exists) is equivalent with a similar formula without quantifiers. An important consequence is the decidability of the theory of real-closed fields.

Statement

A semialgebraic set in Rn is a finite union of sets defined by a finite number of polynomial equations and inequalities, that is by a finite number of statements of the form

p(x_1,\ldots,x_n)=0\,

and

q(x_1,\ldots,x_n)>0\,

for polynomials p and q. We define a projection map π : Rn+1 → Rn by sending a point (x1,...,xn,xn+1) to (x1,...,xn). Then the Tarski–Seidenberg theorem states that if X is a semialgebraic set in Rn+1 for some n > 1, then π(X) is a semialgebraic set in Rn.

Failure with algebraic sets

If we only define sets using polynomial equations and not inequalities then we define algebraic sets rather than semialgebraic sets. For these sets the theorem fails. As a simple example consider the circle in R2 defined by the equation

x^2+y^2-1=0.\,

This is a perfectly good algebraic set, but project it down by sending (x,y) in R2 to x in R and we have the set of points satisfying -1 ≤ x ≤ 1. This is a semialgebraic set as we would expect from the theorem, but it is not an algebraic set.

Relation to structures

This result confirmed that semialgebraic sets in Rn form what is now known as an o-minimal structure on R. These are collections of subsets Sn of Rn for each n ≥ 1 such that we can take finite unions and complements of the subsets in Sn and the result will still be in Sn, moreover the elements of S1 are simply finite unions of intervals and points. The final condition for such a collection to be an o-minimal structure is that the projection map on the first n coordinates from Rn+1 to Rn must send subsets in Sn+1 to subsets in Sn. The Tarski–Seidenberg theorem tells us this holds if Sn is the set of semialgebraic sets in Rn.

See also

External links

Tarski–Seidenberg theorem at PlanetMath.org.

References

This article is issued from Wikipedia - version of the Monday, May 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.