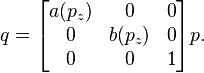Tapering (mathematics)

In mathematics, physics, and theoretical computer graphics, tapering is a kind of shape deformation.[1][2] Just as an affine transformation, such as scaling or shearing, is a first-order model of shape deformation, there also exist higher-order deformations such as tapering, twisting, and bending. Tapering can be thought of as non-constant scaling by a given tapering function. The resultant deformations can be linear or nonlinear.

To create a nonlinear taper, instead of scaling in x and y for all z with constants as in:

q= \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \end{bmatrix} p,

let a and b be functions of z so that:

q= \begin{bmatrix} a(p_z) & 0 & 0 \\ 0 & b(p_z) & 0 \\ 0 & 0 & 1 \end{bmatrix} p.

An example of a linear taper is 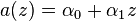a(z) = \alpha_0 + \alpha_1z, and a quadratic taper a(z) = {\alpha}_0 + {\alpha}_1z + {\alpha}_2z^2.

As another example, if the parametric equation of a cube were given by ƒ(t) = (x(t), y(t), z(t)), a nonlinear taper could be applied so that the cube's volume slowly decreases (or tapers) as the function moves in the positive z direction. For the given cube, an example of a nonlinear taper along z would be if, for instance, the function T(z) = 1/(a + bt) were applied to the cube's equation such that ƒ(t) = (T(z)x(t), T(z)y(t), T(z)z(t)), for some real constants a and b.

See also

References

  1. ↑ Shirley, Peter; Ashikhmin, Michael; Marschner, Steve (2009). Fundamentals of Computer Graphics (3rd ed.). CRC Press. p. 426. ISBN 9781568814698.
  2. ↑ Barr, Alan H. (July 1984). "GLOBAL AND LOCAL DEFORMATIONS OF SOLID PRIMITIVES" (PDF). Computer Graphics 18 (3): 21–30. Retrieved 4 May 2015.

External links

This article is issued from Wikipedia - version of the Tuesday, May 05, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.