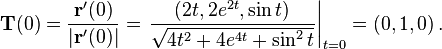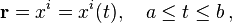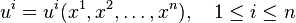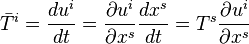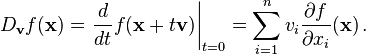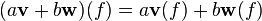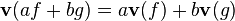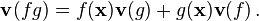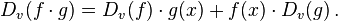Tangent vector

For a more general, but much more technical, treatment of tangent vectors, see tangent space.

In mathematics, a tangent vector is a vector that is tangent to a curve or surface at a given point. Tangent vectors are described in the differential geometry of curves in the context of curves in Rⁿ. More generally, tangent vectors are elements of a tangent space of a differentiable manifold. Tangent vectors can also be described in terms of germs. In other words, a tangent vector at the point $x$ is a linear derivation of the algebra defined by the set of germs at $x$ .

Motivation

Before proceeding to a general definition of the tangent vector, we discuss its use in calculus and its tensor properties.

Calculus

Let 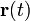$\mathbf{r}(t)$ be a parametric smooth curve. The tangent vector is given by 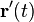$\mathbf{r}^\prime(t)$ , where we have used the a prime instead of the usual dot to indicate differentiation with respect to parameter t.^[1] the unit tangent vector is given by

\mathbf{T}(t)=\frac{\mathbf{r}^\prime(t)}{|\mathbf{r}^\prime(t)|}\,.

Example

Given the curve

\mathbf{r}(t)=\{(1+t^2,e^{2t},\cos{t})|\ t\in\mathbb{R}\}

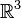in $\mathbb{R}^3$ , the unit tangent vector at time 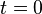$t=0$ is given by

\mathbf{T}(0)=\frac{\mathbf{r}^\prime(0)}{|\mathbf{r}^\prime(0)|}=\left.\frac{(2t,2e^{2t},\sin{t})}{\sqrt{4t^2+4e^{4t}+\sin^2{t}}}\right|_{t=0}=(0,1,0)\,.

Contravariance

If 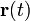$\mathbf{r}(t)$ is given parametrically in the n-dimensional coordinate system xⁱ (here we have used superscripts as an index instead of the usual subscript) by 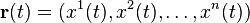$\mathbf{r}(t)=(x^1(t),x^2(t),\ldots,x^n(t))$ or

\mathbf{r}=x^i=x^i(t),\quad a\leq t\leq b\,,

then the tangent vector field $\mathbf{T}=T^i$ is given by

T^i=\frac{dx^i}{dt}\,.

Under a change of coordinates

u^i=u^i(x^1,x^2,\ldots,x^n),\quad 1\leq i\leq n

the tangent vector $\bar{\mathbf{T}}=\bar{T}^i$ in the uⁱ-coordinate system is given by

\bar{T}^i=\frac{du^i}{dt}=\frac{\partial u^i}{\partial x^s}\frac{dx^s}{dt}=T^s\frac{\partial u^i}{\partial x^s}

where we have used the Einstein summation convention. Therefore, a tangent vector of a smooth curve will transform as a contravariant tensor of order one under a change of coordinates.^[2]

Definition

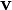Let $f:\mathbb{R}^n\rightarrow\mathbb{R}$ be a differentiable function and let $\mathbf{v}$ be a vector in 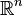$\mathbb{R}^n$ . We define the directional derivative in the 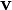$\mathbf{v}$ direction at a point 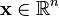$\mathbf{x}\in\mathbb{R}^n$ by

D_\mathbf{v}f(\mathbf{x})=\left.\frac{d}{dt}f(\mathbf{x}+t\mathbf{v})\right|_{t=0}=\sum_{i=1}^{n}v_i\frac{\partial f}{\partial x_i}(\mathbf{x})\,.

The tangent vector at the point 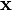$\mathbf{x}$ may then be defined^[3] as

\mathbf{v}(f(\mathbf{x}))\equiv D_\mathbf{v}(f(\mathbf{x}))\,.

Properties

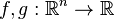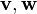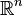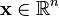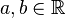Let $f,g:\mathbb{R}^n\rightarrow\mathbb{R}$ be differentiable functions, let $\mathbf{v},\mathbf{w}$ be tangent vectors in $\mathbb{R}^n$ at $\mathbf{x}\in\mathbb{R}^n$ , and let $a,b\in\mathbb{R}$ . Then

$(a\mathbf{v}+b\mathbf{w})(f)=a\mathbf{v}(f)+b\mathbf{w}(f)$
$\mathbf{v}(af+bg)=a\mathbf{v}(f)+b\mathbf{v}(g)$
$\mathbf{v}(fg)=f(\mathbf{x})\mathbf{v}(g)+g(\mathbf{x})\mathbf{v}(f)\,.$

Tangent Vector on Manifolds

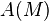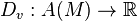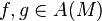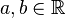Let $M$ be a differentiable manifold and let $A(M)$ be the algebra of real-valued differentiable functions $M$ . Then the tangent vector to $M$ at a point $x$ in the manifold is given by the derivation $D_v:A(M)\rightarrow\mathbb{R}$ which shall be linear — i.e., for any $f,g\in A(M)$ and $a,b\in\mathbb{R}$ we have

D_v(af+bg)=aD_v(f)+bD_v(g)\,.

Note that the derivation will by definition have the Leibniz property

D_v(f\cdot g)=D_v(f)\cdot g(x)+f(x)\cdot D_v(g)\,.

References

↑ J. Stewart (2001)
↑ D. Kay (1988)
↑ A. Gray (1993)

Bibliography

Gray, Alfred (1993), Modern Differential Geometry of Curves and Surfaces, Boca Raton: CRC Press .
Stewart, James (2001), Calculus: Concepts and Contexts, Australia: Thomson/Brooks/Cole .
Kay, David (1988), Schaums Outline of Theory and Problems of Tensor Calculus, New York: McGraw-Hill .

This article is issued from Wikipedia - version of the Tuesday, January 19, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.