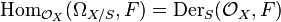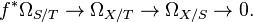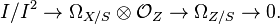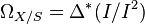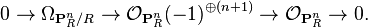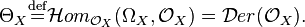Cotangent sheaf

In algebraic geometry, given a morphism f: X → S of schemes, the cotangent sheaf on X is the sheaf of \mathcal{O}_X-modules that represents (or classifies) S-derivations [1] in the sense: for any \mathcal{O}_X-modules F, there is an isomorphism

\operatorname{Hom}_{\mathcal{O}_X}(\Omega_{X/S}, F) = \operatorname{Der}_S(\mathcal{O}_X, F)

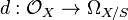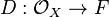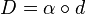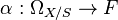that depends naturally on F. In other words, the cotangent sheaf is characterized by the universal property: there is the differential d: \mathcal{O}_X \to \Omega_{X/S} such that any S-derivation D: \mathcal{O}_X \to F factors as D = \alpha \circ d with some \alpha: \Omega_{X/S} \to F.

In the case X and S are affine schemes, the above definition means that 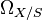\Omega_{X/S} is the module of Kähler differentials. The standard way to construct a cotangent sheaf (e.g., Hartshorne, Ch II. § 8) is through a diagonal morphism (which amounts to gluing modules of Kähler differentials on affine charts to get the globally-defined cotangent sheaf.) The dual module of the cotangent sheaf on a scheme X is called the tangent sheaf on X and is sometimes denoted by 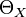\Theta_X.[2]

There are two important exact sequences:

  1. If S →T is a morphism of schemes, then
    f^* \Omega_{S/T} \to \Omega_{X/T} \to \Omega_{X/S} \to 0.
  2. If Z is a closed subscheme of X with ideal sheaf I, then
    I/I^2 \to \Omega_{X/S} \otimes \mathcal{O}_Z \to \Omega_{Z/S} \to 0.[3][4]

The cotangent sheaf is closely related to smoothness of a variety or scheme. For example, an algebraic variety is smooth of dimension n if and only if ΩX is a locally free sheaf of rank n.[5]

Construction through a diagonal morphism

Let 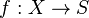f: X \to S be a morphism of schemes as in the introduction and Δ: X → X ×S X the diagonal morphism. Then the image of Δ is locally closed; i.e., closed in some open subset W of X ×S X (the image is closed if and only if f is separated). Let I be the ideal sheaf of Δ(X) in W. One then puts:

\Omega_{X/S} = \Delta^* (I/I^2)

and checks this sheaf of modules satisfies the required universal property of a cotangent sheaf (Hartshorne, Ch II. Remark 8.9.2). The construction shows in particular that the cotangent sheaf is quasi-coherent. It is coherent if S is Noetherian and f is of finite type.

Relation to a tautological line bundle

Main article: Euler sequence

The cotangent sheaf on a projective space is related to the tautological line bundle O(-1) by the following exact sequence: writing 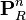\mathbf{P}^n_R for the projective space over a ring R,

0 \to \Omega_{\mathbf{P}^n_R/R} \to \mathcal{O}_{\mathbf{P}^n_R}(-1)^{\oplus(n+1)} \to \mathcal{O}_{\mathbf{P}^n_R} \to 0.

(See also Chern class#Complex projective space.)

Cotangent stack

For this notion, see § 1 of

A. Beilinson and V. Drinfeld, Quantization of Hitchin’s integrable system and Hecke eigensheaves [6]

There, the cotangent stack on an algebraic stack X is defined as the relative Spec of the symmetric algebra of the tangent sheaf on X. (Note: in general, if E is a locally free sheaf of finite rank, 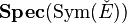\mathbf{Spec}(\operatorname{Sym}(\check{E})) is the algebraic vector bundle corresponding to E.)

See also: Hitchin fibration (the cotangent stack of 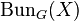\operatorname{Bun}_G(X) is the total space of the Hitchin fibration.)

Notes

  1. ↑ http://stacks.math.columbia.edu/tag/08RL
  2. ↑ In concise terms, this means:
    \Theta_X \overset{\mathrm{def}} = \mathcal{H}om_{\mathcal{O}_X}(\Omega_X, \mathcal{O}_X) = \mathcal{D}er(\mathcal{O}_X).
  3. ↑ Hartshorne, Ch. II, Proposition 8.12.
  4. ↑ http://mathoverflow.net/questions/79956/jacobian-criterion-for-smoothness-of-schemes as well as (Hartshorne, Ch. II, Theorem 8.17.)
  5. ↑ Hartshorne, Ch. II, Theorem 8.15.
  6. ↑ see also: § 3 of http://www.math.harvard.edu/~gaitsgde/grad_2009/SeminarNotes/Sept22(Dmodstack1).pdf

See also

References

External links


This article is issued from Wikipedia - version of the Monday, January 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.