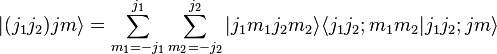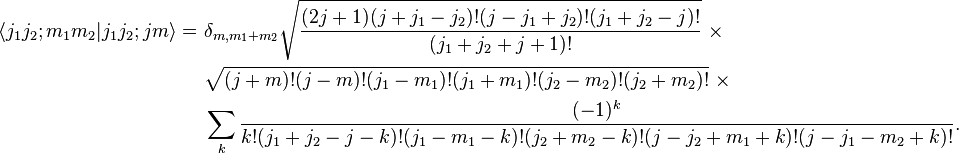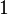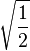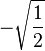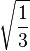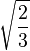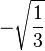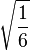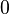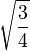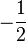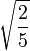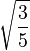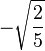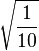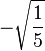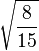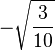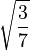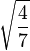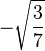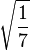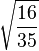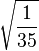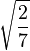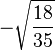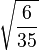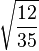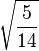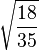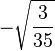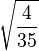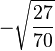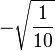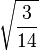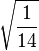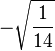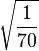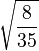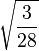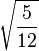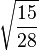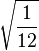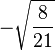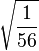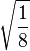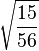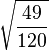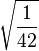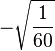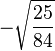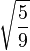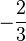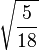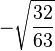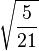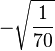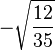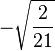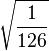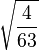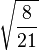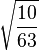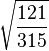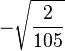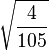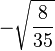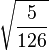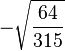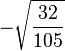Table of Clebsch–Gordan coefficients
This is a table of Clebsch–Gordan coefficients used for adding angular momentum values in quantum mechanics. The overall sign of the coefficients for each set of constant 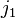 ,
, 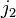 ,
, 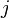 is arbitrary to some degree and has been fixed according to the Condon-Shortley and Wigner sign convention as discussed by Baird and Biedenharn.[1] Tables with the same sign convention may be found in the Particle Data Group's Review of Particle Properties[2] and in online tables.[3]
is arbitrary to some degree and has been fixed according to the Condon-Shortley and Wigner sign convention as discussed by Baird and Biedenharn.[1] Tables with the same sign convention may be found in the Particle Data Group's Review of Particle Properties[2] and in online tables.[3]
Formulation
The Clebsch–Gordan coefficients are the solutions to
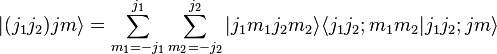
Explicitly:
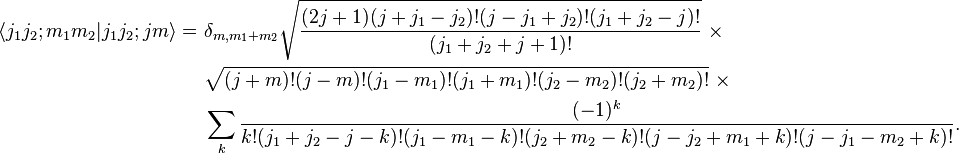
The summation is extended over all integer k for which the argument of every factorial is nonnegative.[4]
For brevity, solutions with m < 0 and j1 < j2 are omitted. They may be calculated using the simple relations
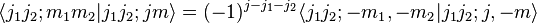 .
.
and
 .
.
A complete list [5]
j2=0
When j2 = 0, the Clebsch–Gordan coefficients are given by 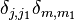 .
.
j1=1/2, j2=1/2
| m=1 |
j |
| m1, m2 |
|
1 |
| 1/2, 1/2 |
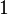 |
|
j1=1, j2=1/2
| m=3/2 |
j |
| m1, m2 |
|
3/2 |
| 1, 1/2 |
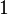 |
|
j1=1, j2=1
| m=2 |
j |
| m1, m2 |
|
2 |
| 1, 1 |
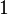 |
|
j1=3/2, j2=1/2
| m=2 |
j |
| m1, m2 |
|
2 |
| 3/2, 1/2 |
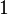 |
|
j1=3/2, j2=1
| m=5/2 |
j |
| m1, m2 |
|
5/2 |
| 3/2, 1 |
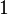 |
|
| m=1/2 |
j |
| m1, m2 |
|
5/2 |
3/2 |
1/2 |
| 3/2, -1 |
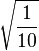 |
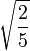 |
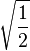 |
| 1/2, 0 |
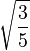 |
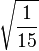 |
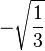 |
| -1/2, 1 |
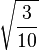 |
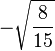 |
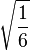 |
|
j1=3/2, j2=3/2
| m=3 |
j |
| m1, m2 |
|
3 |
| 3/2, 3/2 |
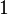 |
|
| m=1 |
j |
| m1, m2 |
|
3 |
2 |
1 |
| 3/2, -1/2 |
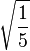 |
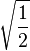 |
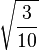 |
| 1/2, 1/2 |
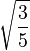 |
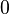 |
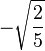 |
| -1/2, 3/2 |
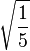 |
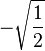 |
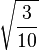 |
|
| m=0 |
j |
| m1, m2 |
|
3 |
2 |
1 |
0 |
| 3/2, -3/2 |
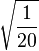 |
 |
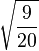 |
 |
| 1/2, -1/2 |
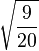 |
 |
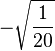 |
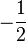 |
| -1/2, 1/2 |
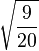 |
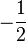 |
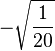 |
 |
| -3/2, 3/2 |
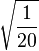 |
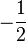 |
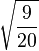 |
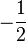 |
|
j1=2, j2=1/2
| m=5/2 |
j |
| m1, m2 |
|
5/2 |
| 2, 1/2 |
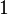 |
|
j1=2, j2=1
| m=3 |
j |
| m1, m2 |
|
3 |
| 2, 1 |
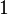 |
|
j1=2, j2=3/2
| m=7/2 |
j |
| m1, m2 |
|
7/2 |
| 2, 3/2 |
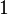 |
|
| m=3/2 |
j |
| m1, m2 |
|
7/2 |
5/2 |
3/2 |
| 2, -1/2 |
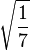 |
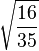 |
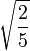 |
| 1, 1/2 |
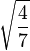 |
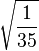 |
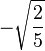 |
| 0, 3/2 |
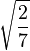 |
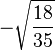 |
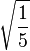 |
|
| m=1/2 |
j |
| m1, m2 |
|
7/2 |
5/2 |
3/2 |
1/2 |
| 2, -3/2 |
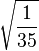 |
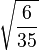 |
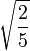 |
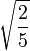 |
| 1, -1/2 |
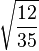 |
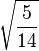 |
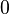 |
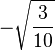 |
| 0, 1/2 |
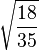 |
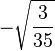 |
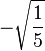 |
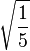 |
| -1, 3/2 |
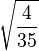 |
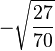 |
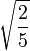 |
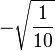 |
|
j1=2, j2=2
| m=4 |
j |
| m1, m2 |
|
4 |
| 2, 2 |
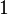 |
|
| m=1 |
j |
| m1, m2 |
|
4 |
3 |
2 |
1 |
| 2, -1 |
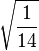 |
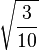 |
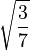 |
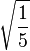 |
| 1, 0 |
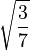 |
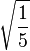 |
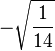 |
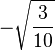 |
| 0, 1 |
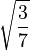 |
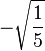 |
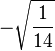 |
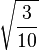 |
| -1, 2 |
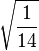 |
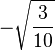 |
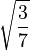 |
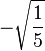 |
|
| m=0 |
j |
| m1, m2 |
|
4 |
3 |
2 |
1 |
0 |
| 2, -2 |
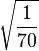 |
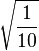 |
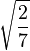 |
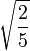 |
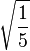 |
| 1, -1 |
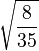 |
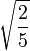 |
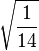 |
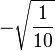 |
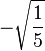 |
| 0, 0 |
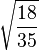 |
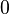 |
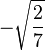 |
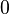 |
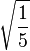 |
| -1, 1 |
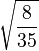 |
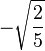 |
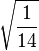 |
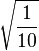 |
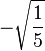 |
| -2, 2 |
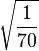 |
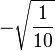 |
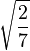 |
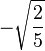 |
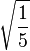 |
|
j1=5/2, j2=1/2
| m=3 |
j |
| m1, m2 |
|
3 |
| 5/2, 1/2 |
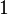 |
|
j1=5/2, j2=1
| m=7/2 |
j |
| m1, m2 |
|
7/2 |
| 5/2, 1 |
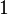 |
|
| m=3/2 |
j |
| m1, m2 |
|
7/2 |
5/2 |
3/2 |
| 5/2, -1 |
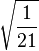 |
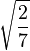 |
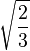 |
| 3/2, 0 |
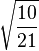 |
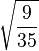 |
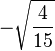 |
| 1/2, 1 |
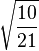 |
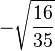 |
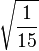 |
|
| m=1/2 |
j |
| m1, m2 |
|
7/2 |
5/2 |
3/2 |
| 3/2, -1 |
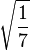 |
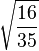 |
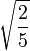 |
| 1/2, 0 |
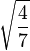 |
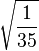 |
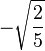 |
| -1/2, 1 |
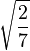 |
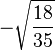 |
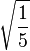 |
|
j1=5/2, j2=3/2
| m=4 |
j |
| m1, m2 |
|
4 |
| 5/2, 3/2 |
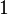 |
|
| m=2 |
j |
| m1, m2 |
|
4 |
3 |
2 |
| 5/2, -1/2 |
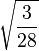 |
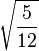 |
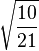 |
| 3/2, 1/2 |
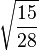 |
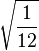 |
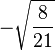 |
| 1/2, 3/2 |
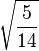 |
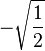 |
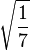 |
|
| m=1 |
j |
| m1, m2 |
|
4 |
3 |
2 |
1 |
| 5/2, -3/2 |
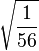 |
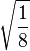 |
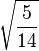 |
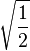 |
| 3/2, -1/2 |
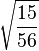 |
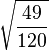 |
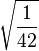 |
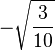 |
| 1/2, 1/2 |
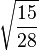 |
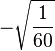 |
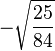 |
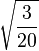 |
| -1/2, 3/2 |
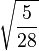 |
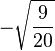 |
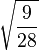 |
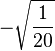 |
|
| m=0 |
j |
| m1, m2 |
|
4 |
3 |
2 |
1 |
| 3/2, -3/2 |
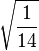 |
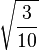 |
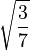 |
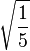 |
| 1/2, -1/2 |
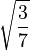 |
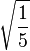 |
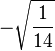 |
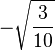 |
| -1/2, 1/2 |
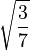 |
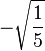 |
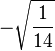 |
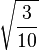 |
| -3/2, 3/2 |
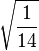 |
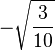 |
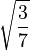 |
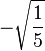 |
|
j1=5/2, j2=2
| m=9/2 |
j |
| m1, m2 |
|
9/2 |
| 5/2, 2 |
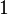 |
|
| m=5/2 |
j |
| m1, m2 |
|
9/2 |
7/2 |
5/2 |
| 5/2, 0 |
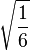 |
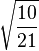 |
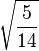 |
| 3/2, 1 |
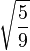 |
 |
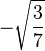 |
| 1/2, 2 |
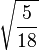 |
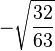 |
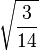 |
|
| m=3/2 |
j |
| m1, m2 |
|
9/2 |
7/2 |
5/2 |
3/2 |
| 5/2, -1 |
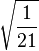 |
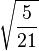 |
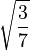 |
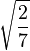 |
| 3/2, 0 |
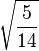 |
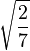 |
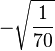 |
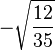 |
| 1/2, 1 |
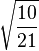 |
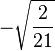 |
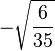 |
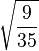 |
| -1/2, 2 |
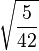 |
 |
 |
 |
|
| m=1/2 |
j |
| m1, m2 |
|
9/2 |
7/2 |
5/2 |
3/2 |
1/2 |
| 5/2, -2 |
 |
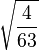 |
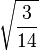 |
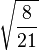 |
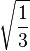 |
| 3/2, -1 |
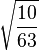 |
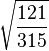 |
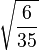 |
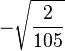 |
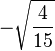 |
| 1/2, 0 |
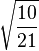 |
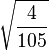 |
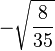 |
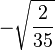 |
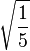 |
| -1/2, 1 |
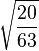 |
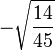 |
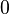 |
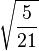 |
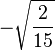 |
| -3/2, 2 |
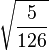 |
 |
 |
 |
 |
|
SU(N) Clebsch–Gordan coefficients
Algorithms to produce Clebsch–Gordan coefficients for higher values of 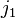 and
and 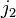 , or for the su(N) algebra instead of su(2), are known.[6]
A web interface for tabulating SU(N) Clebsch-Gordan coefficients is readily available.
, or for the su(N) algebra instead of su(2), are known.[6]
A web interface for tabulating SU(N) Clebsch-Gordan coefficients is readily available.
References
- ↑ Baird, C.E.; L. C. Biedenharn (October 1964). "On the Representations of the Semisimple Lie Groups. III. The Explicit Conjugation Operation for SUn". J. Math. Phys. 5: 1723–1730. Bibcode:1964JMP.....5.1723B. doi:10.1063/1.1704095. Retrieved 2007-12-20.
- ↑ Hagiwara, K.; et al. (July 2002). "Review of Particle Properties" (PDF). Phys. Rev. D 66: 010001. Bibcode:2002PhRvD..66a0001H. doi:10.1103/PhysRevD.66.010001. Retrieved 2007-12-20.
- ↑ Mathar, Richard J. (2006-08-14). "SO(3) Clebsch Gordan coefficients" (text). Retrieved 2012-10-15.
- ↑ (2.41), p. 172, Quantum Mechanics: Foundations and Applications, Arno Bohm, M. Loewe, New York: Springer-Verlag, 3rd ed., 1993, ISBN 0-387-95330-2.
- ↑ Weisbluth, Michael (1978). Atoms and molecules. ACADEMIC PRESS. p. 28. ISBN 0-12-744450-5. Table 1.4 resumes the most common.
- ↑ Alex, A.; M. Kalus; A. Huckleberry; J. von Delft (February 2011). "A numerical algorithm for the explicit calculation of SU(N) and SL(N,C) Clebsch-Gordan coefficients". J. Math. Phys. 82: 023507. arXiv:1009.0437. Bibcode:2011JMP....52b3507A. doi:10.1063/1.3521562. Retrieved 2011-04-13.
External links
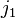 ,
, 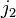 ,
, 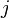 is arbitrary to some degree and has been fixed according to the Condon-Shortley and Wigner sign convention as discussed by Baird and Biedenharn.[1] Tables with the same sign convention may be found in the Particle Data Group's Review of Particle Properties[2] and in online tables.[3]
is arbitrary to some degree and has been fixed according to the Condon-Shortley and Wigner sign convention as discussed by Baird and Biedenharn.[1] Tables with the same sign convention may be found in the Particle Data Group's Review of Particle Properties[2] and in online tables.[3]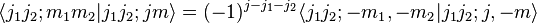 .
. .
.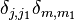 .
.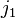 and
and 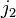 , or for the su(N) algebra instead of su(2), are known.[6]
A web interface for tabulating SU(N) Clebsch-Gordan coefficients is readily available.
, or for the su(N) algebra instead of su(2), are known.[6]
A web interface for tabulating SU(N) Clebsch-Gordan coefficients is readily available.