t-J model

The t-J model was first derived in 1977 from the Hubbard model by Józef Spałek. The model describes strongly correlated electron systems. It is used to calculate high temperature superconductivity states in doped antiferromagnets.

The t-J Hamiltonian is:

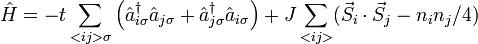
$\hat H = -t\sum_{<ij>\sigma}\left(\hat a^\dagger_{i\sigma} \hat a_{j\sigma} + \hat a^\dagger_{j\sigma} \hat a_{i\sigma}\right) + J\sum_{<ij>}(\vec S_{i}\cdot \vec S_{j}-n_in_j/4)$

where

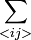$\sum_{<ij>}$ - sum over nearest-neighbor sites i and j,
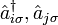$\hat a^\dagger_{i\sigma} , \hat a_{j\sigma}$ - fermionic creation and annihilation operators,
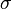$\sigma$ - spin polarization,
$t$ - hopping integral
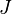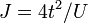$J$ - coupling constant $J = 4t^2/U$ ,
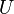$U$ - coulomb repulsion,
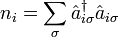$n_{i} = \sum_{\sigma}\hat a^\dagger_{i\sigma}\hat a_{i\sigma}$ - particle number at the site i, and
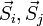$\vec S_i, \vec S_j$ - spins on the sites i and j.

Connection to the high-temperature superconductivity

The Hamiltonian of the 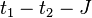$t_{1}-t_{2}-J$ model in terms of $CP^{1}$ generalized model reads ^[1]

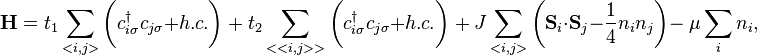
$\mathbf{H} = t_1 \sum\limits_{<i,j>} \bigg( c_{i\sigma}^{\dagger} c_{j\sigma} + h.c. \bigg) \ + \ t_2 \sum\limits_{<<i,j>>} \bigg( c_{i\sigma}^{\dagger} c_{j\sigma} + h.c. \bigg) \ + \ J \sum\limits_{<i,j>} \bigg( \mathbf{S}_{i} \cdot \mathbf{S}_{j} - \frac{1}{4} n_{i} n_{j} \bigg) - \ \mu\sum\limits_{i} n_{i} ,$

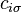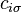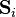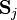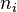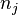where fermionic operators $c_{i\sigma}$ , $c_{i\sigma}$ , the spin operators $\mathbf{S}_i$ and $\mathbf{S}_j$ , number operators $n_{i}$ and $n_{j}$ act on restricted Hilbert space and the doubly-occupied states are excluded. The sums in above mentioned equation are over all sites of a (2-d) square lattice, where 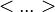$<...>$ and 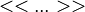$<<...>>$ denote nearest and next-to-the-nearest neighbors, respectively.

References

↑ $\mathbf{\mathit{CP^{1}}}$

Lectures on Correlation and Magnetism, [Patrik Fazekas],[page no. :199]
t-J model then and now: A personal perspective from the pioneering times, Józef Spałek, arXiv:0706.4236

This article is issued from Wikipedia - version of the Wednesday, February 03, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.