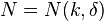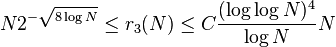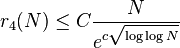Szemerédi's theorem

In arithmetic combinatorics, Szemerédi's theorem is a result concerning arithmetic progressions in subsets of the integers. In 1936, Erdős and Turán conjectured[1] that every set of integers A with positive natural density contains a k term arithmetic progression for every k. Endre Szemerédi proved the conjecture in 1975.

Statement

A subset A of the natural numbers is said to have positive upper density if

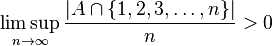\limsup_{n \to \infty}\frac{|A\cap \{1, 2, 3, \dotsc, n\}|}{n} > 0.

Szemerédi's theorem asserts that a subset of the natural numbers with positive upper density contains infinite arithmetic progressions of length k for all positive integers k.

An often-used equivalent finitary version of the theorem states that for every positive integer k and real number \delta \in (0, 1], there exists a positive integer

N = N(k,\delta)\,

such that every subset of {1, 2, ..., N} of size at least δN contains an arithmetic progression of length k.

Another formulation uses the function rk(N), the size of the largest subset of {1, 2, ..., N} without an arithmetic progression of length k. Szemerédi's theorem is equivalent to the asymptotic bound

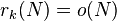r_k(N) = o(N).

That is, rk(N) grows less than linearly with N.

History

Van der Waerden's theorem, a precursor of Szemerédi's theorem, was proven in 1927.

The cases k = 1 and k = 2 of Szemerédi's theorem are trivial. The case k = 3 was established in 1953 by Klaus Roth[2] via an adaptation of the Hardy–Littlewood circle method. The case k = 4 was established in 1969 by Endre Szemerédi[3] via a combinatorial method. Using an approach similar to the one he used for the case k = 3, Roth[4] gave a second proof for this in 1972.

Finally, the case of general k was settled in 1975, also by Szemerédi,[5] via an ingenious and complicated extension of the previous combinatorial argument (called "a masterpiece of combinatorial reasoning" by Erdős[6]). Several other proofs are now known, the most important being those by Hillel Furstenberg[7][8] in 1977, using ergodic theory, and by Timothy Gowers[9] in 2001, using both Fourier analysis and combinatorics. Terence Tao has called the various proofs of Szemerédi's theorem a "Rosetta stone" for connecting disparate fields of mathematics.[10]

Quantitative bounds

It is an open problem to determine the exact growth rate of rk(N). The best known general bounds are

CN\exp(-n2^{(n - 1)/2}\sqrt[n]{\log N} + \frac{1}{2n}\log \log N) \leq r_k(N) \leq \frac{N}{(\log \log N)^{2^{-2^{k + 9}}}}.

The lower bound is due to O'Bryant[11] building on the work of Behrend,[12] Rankin,[13] and Elkin.[14][15] The upper bound is due to Gowers.[9]

For small k, there are tighter bounds than the general case. When k = 3, Bourgain,[16][17] Heath-Brown,[18] Szemerédi,[19] and Sanders[20] provided increasingly smaller upper bounds. The current best bounds are

N2^{-\sqrt{8\log N}} \leq r_3(N) \leq C\frac{(\log \log N)^4}{\log N}N

due to O'Bryant[11] and Bloom[21] respectively.

For k = 4, Green and Tao[22] proved the bound

r_4(N) \leq C\frac{N}{e^{c\sqrt{\log\log N}}}

for some c > 0.

Extensions and generalizations

A multidimensional generalization of Szemerédi's theorem was first proven by Furstenberg and Katznelson using ergodic theory.[23] Gowers,[24] Rödl-Skokan[25][26] with Nagle-Rödl-Schacht,[27] and Tao[28] provided combinatorial proofs.

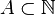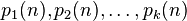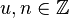Leibman and Bergelson[29] generalized Szemerédi's to polynomial progressions: If A \subset \mathbb{N} is a set with positive upper density and p_1(n),p_2(n),\dotsc,p_k(n) are integer-valued polynomials such that p_i(k) = 0, then there are infinitely many u, n \in \mathbb{Z} such that 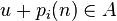u + p_i(n) \in A for all 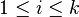1 \leq i \leq k. Leibman and Bergelson's result also holds in a multidimensional setting.

The finitary version of Szemerédi's theorem can be generalized to finite additive groups including vector spaces over finite fields.[30] The finite field analog can be used as a model for understanding the theorem in the natural numbers.[31]

The Green–Tao theorem asserts the prime numbers contain arbitrary long arithmetic progressions. It is not implied by Szemerédi's theorem because the primes have density 0 in the natural numbers. As part of their proof, Green and Tao introduced a "relative" Szemerédi theorem which applies to subsets of the integers (even those with 0 density) satisfying certain pseudorandomness conditions. A more general relative Szemerédi theorem has since been given by Conlon, Fox, and Zhao.[32][33]

The Erdős conjecture on arithmetic progressions would imply both Szemerédi's theorem and the Green–Tao theorem.

See also

Notes

  1. ↑ Erdős, Paul; Turán, Paul (1936). "On some sequences of integers" (PDF). Journal of the London Mathematical Society 11 (4): 261–264. doi:10.1112/jlms/s1-11.4.261. MR 1574918.
  2. ↑ Roth, Klaus Friedrich (1953). "On certain sets of integers". Journal of the London Mathematical Society 28 (1): 104–109. doi:10.1112/jlms/s1-28.1.104. MR 0051853. Zbl 0050.04002.
  3. ↑ Szemerédi, Endre (1969). "On sets of integers containing no four elements in arithmetic progression". Acta Math. Acad. Sci. Hung. 20: 89–104. doi:10.1007/BF01894569. MR 0245555. Zbl 0175.04301.
  4. ↑ Roth, Klaus Friedrich (1972). "Irregularities of sequences relative to arithmetic progressions, IV". Periodica Math. Hungar. 2: 301–326. doi:10.1007/BF02018670. MR 0369311.
  5. ↑ Szemerédi, Endre (1975). "On sets of integers containing no k elements in arithmetic progression" (PDF). Acta Arithmetica 27: 199–245. MR 0369312. Zbl t0303.10056.
  6. ↑ Erdős, Paul (2013). "Some of My Favorite Problems and Results". In Graham, Ronald L.; Nešetřil, Jaroslav; Butler, Steve. The Mathematics of Paul Erdős I (Second ed.). New York: Springer. pp. 51–70. doi:10.1007/978-1-4614-7258-2_3. ISBN 978-1-4614-7257-5. MR 1425174.
  7. ↑ Furstenberg, Hillel (1977). "Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions". J. D'Analyse Math. 31: 204–256. doi:10.1007/BF02813304. MR 0498471..
  8. ↑ Furstenberg, Hillel; Katznelson, Yitzhak; Ornstein, Donald Samuel (1982). "The ergodic theoretical proof of Szemerédi’s theorem". Bull. Amer. Math. Soc. 7 (3): 527–552. doi:10.1090/S0273-0979-1982-15052-2. MR 0670131.
  9. 1 2 Gowers, Timothy (2001). "A new proof of Szemerédi's theorem". Geom. Funct. Anal. 11 (3): 465–588. doi:10.1007/s00039-001-0332-9. MR 1844079.
  10. ↑ Tao, Terence (2007). "The dichotomy between structure and randomness, arithmetic progressions, and the primes". In Sanz-Solé, Marta; Soria, Javier; Varona, Juan Luis; Verdera, Joan. International Congress of Mathematicians 1. Zürich: European Mathematical Society. pp. 581–608. arXiv:math/0512114. doi:10.4171/022-1/22. MR 2334204.
  11. 1 2 O'Bryant, Kevin (2011). "Sets of integers that do not contain long arithmetic progressions". Electronic Journal of Combinatorics 18 (1). MR 2788676.
  12. ↑ Behrend, Felix A. (1946). "On the sets of integers which contain no three terms in arithmetic progression". Proceedings of the National Academy of Sciences 23 (12): 331–332. doi:10.1073/pnas.32.12.331. MR 0018694. Zbl 0060.10302.
  13. ↑ Rankin, Robert A. (1962). "Sets of integers containing not more than a given number of terms in arithmetical progression". Proc. Roy. Soc. Edinburgh Sect. A 65: 332–344. MR 0142526. Zbl 0104.03705.
  14. ↑ Elkin, Michael (2011). "An improved construction of progression-free sets". Israel Journal of Mathematics 184 (1): 93–128. doi:10.1007/s11856-011-0061-1. MR 2823971.
  15. ↑ Green, Ben; Wolf, Julia (2010). "A note on Elkin's improvement of Behrend's construction". In Chudnovsky, David; Chudnovsky, Gregory. Additive number theory. Festschrift in honor of the sixtieth birthday of Melvyn B. Nathanson. New York: Springer. pp. 141–144. doi:10.1007/978-0-387-68361-4_9. ISBN 978-0-387-37029-3. MR 2744752.
  16. ↑ Bourgain, Jean (1999). "On triples in arithmetic progression". Geom. Funct. Anal. 9 (5): 968–984. doi:10.1007/s000390050105. MR 1726234.
  17. ↑ Bourgain, Jean (2008). "Roth's theorem on progressions revisited". J. Anal. Math. 104 (1): 155–192. doi:10.1007/s11854-008-0020-x. MR 2403433.
  18. ↑ Heath-Brown, Roger (1987). "Integer sets containing no arithmetic progressions". Journal of the London Mathematical Society 35 (3): 385–394. doi:10.1112/jlms/s2-35.3.385. MR 889362.
  19. ↑ Szemerédi, Endre (1990). "Integer sets containing no arithmetic progressions". Acta Math. Hungar. 56 (1-2): 155–158. doi:10.1007/BF01903717. MR 1100788.
  20. ↑ Sanders, Tom (2011). "On Roth's theorem on progressions". Annals of Mathematics 174 (1): 619–636. doi:10.4007/annals.2011.174.1.20. MR 2811612.
  21. ↑ Bloom, Thomas F. (2014). "A quantitative improvement for Roth's theorem on arithmetic progressions". arXiv:1405.5800.
  22. ↑ Green, Ben; Tao, Terence (2009). "New bounds for Szemeredi's theorem. II. A new bound for r4(N)". In Chen, William W. L.; Gowers, Timothy; Halberstam, Heini; Schmidt, Wolfgang; Vaughan, Robert Charles. Analytic number theory. Essays in honour of Klaus Roth on the occasion of his 80th birthday. Cambridge: Cambridge University Press. pp. 180–204. arXiv:math/0610604. ISBN 978-0-521-51538-2. MR 2508645. Zbl 1158.11007.
  23. ↑ Furstenberg, Hillel; Katznelson, Yitzhak (1978). "An ergodic Szemerédi theorem for commuting transformations". Journal d'Analyse Mathématique 38 (1): 275–291. doi:10.1007/BF02790016. MR 531279.
  24. ↑ Gowers, Timothy (2007). "Hypergraph regularity and the multidimensional Szemerédi theorem". Ann. of Math. 166 (3): 897–946. doi:10.4007/annals.2007.166.897. MR 2373376.
  25. ↑ Rödl, Vojtěch; Skokan, Jozef (2004). "Regularity lemma for k-uniform hypergraphs". Random Structures Algorithms 25 (1): 1–42. doi:10.1002/rsa.20017. MR 2069663.
  26. ↑ Rödl, Vojtěch; Skokan, Jozef (2006). "Applications of the regularity lemma for uniform hypergraphs". Random Structures Algorithms 28 (2): 180–194. doi:10.1002/rsa.20108. MR 2198496.
  27. ↑ Nagle, Brendan; Rödl, Vojtěch; Schacht, Mathias (2006). "The counting lemma for regular k-uniform hypergraphs". Random Structures Algorithms 28 (2): 113–179. doi:10.1002/rsa.20117. MR 2198495.
  28. ↑ Tao, Terence (2006). "A variant of the hypergraph removal lemma". Journal of Combinatorial Theory. Series A 113 (7): 1257–1280. doi:10.1016/j.jcta.2005.11.006. MR 2259060.
  29. ↑ Bergelson, Vitaly; Leibman, Alexander (1996). "Polynomial extensions of van der Waerden's and Szemerédi's theorems". Journal of the American Mathematical Society 9 (3): 725–753. doi:10.1090/S0894-0347-96-00194-4. MR 1325795.
  30. ↑ Furstenberg, Hillel; Katznelson, Yitzhak (1991). "A density version of the Hales–Jewett theorem". Journal d'Analyse Mathématique 57 (1): 64–119. doi:10.1007/BF03041066. MR 1191743.
  31. ↑ Wolf, Julia (2015). "Finite field models in arithmetic combinatorics—ten years on". Finite Fields and Their Applications 32: 233–274. doi:10.1016/j.ffa.2014.11.003. MR 3293412.
  32. ↑ Conlon, David; Fox, Jacob; Zhao, Yufei (2015). "A relative Szemerédi theorem". Geometric and Functional Analysis 25 (3): 733–762. arXiv:1305.5440. doi:10.1007/s00039-015-0324-9. MR 3361771.
  33. ↑ Zhao, Yufei (2014). "An arithmetic transference proof of a relative Szemerédi theorem". Mathematical Proceedings of the Cambridge Philosophical Society 156 (2): 255–261. doi:10.1017/S0305004113000662. MR 3177868.

Further reading

External links

This article is issued from Wikipedia - version of the Wednesday, February 03, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.