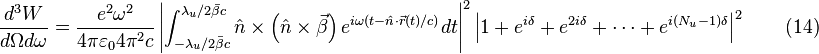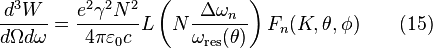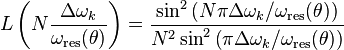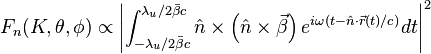Synchrotron radiation
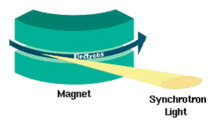
The electromagnetic radiation emitted when charged particles are accelerated radially (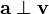 ) is called synchrotron radiation. It is produced, for example, in synchrotrons using bending magnets, undulators and/or wigglers. It is similar to cyclotron radiation except that synchrotron radiation is generated by the acceleration of ultrarelativistic charged particles through magnetic fields. Synchrotron radiation may be achieved artificially in synchrotrons or storage rings, or naturally by fast electrons moving through magnetic fields. The radiation produced in this way has a characteristic polarization and the frequencies generated can range over the entire electromagnetic spectrum.
) is called synchrotron radiation. It is produced, for example, in synchrotrons using bending magnets, undulators and/or wigglers. It is similar to cyclotron radiation except that synchrotron radiation is generated by the acceleration of ultrarelativistic charged particles through magnetic fields. Synchrotron radiation may be achieved artificially in synchrotrons or storage rings, or naturally by fast electrons moving through magnetic fields. The radiation produced in this way has a characteristic polarization and the frequencies generated can range over the entire electromagnetic spectrum.

History

Synchrotron radiation was named after its discovery in a General Electric synchrotron accelerator built in 1946 and announced in May 1947 by Frank Elder, Anatole Gurewitsch, Robert Langmuir, and Herb Pollock in a letter entitled "Radiation from Electrons in a Synchrotron".[1] Pollock recounts:
- "On April 24, Langmuir and I were running the machine and as usual were trying to push the electron gun and its associated pulse transformer to the limit. Some intermittent sparking had occurred and we asked the technician to observe with a mirror around the protective concrete wall. He immediately signaled to turn off the synchrotron as "he saw an arc in the tube." The vacuum was still excellent, so Langmuir and I came to the end of the wall and observed. At first we thought it might be due to Cherenkov radiation, but it soon became clearer that we were seeing Ivanenko and Pomeranchuk radiation."[2]
Properties of synchrotron radiation
- Broad Spectrum (which covers from microwaves to hard X-rays): the users can select the wavelength required for their experiment.
- High Flux: high intensity photon beam allows rapid experiments or use of weakly scattering crystals.
- High Brilliance: highly collimated photon beam generated by a small divergence and small size source (spatial coherence)
- High Stability: submicron source stability
- Polarization: both linear and circular
- Pulsed Time Structure: pulsed length down to tens of picoseconds allows the resolution of process on the same time scale.
Emission mechanism
When high-energy particles are in rapid motion, including electrons forced to travel in a curved path by a magnetic field, synchrotron radiation is produced. This is similar to a radio antenna, but with the difference that, in theory, the relativistic speed will change the observed frequency due to the Doppler effect by the Lorentz factor,  .
Relativistic length contraction then bumps the frequency observed in the lab by another factor of
.
Relativistic length contraction then bumps the frequency observed in the lab by another factor of  , thus multiplying the GHz frequency of the resonant cavity that accelerates the electrons into the X-ray range. The radiated power is given by the relativistic Larmor formula while the force on the emitting electron is given by the Abraham–Lorentz–Dirac force.
The radiation pattern can be distorted from an isotropic dipole pattern into an extremely forward-pointing cone of radiation. Synchrotron radiation is the brightest artificial source of X-rays.
The planar acceleration geometry appears to make the radiation linearly polarized when observed in the orbital plane, and circularly polarized when observed at a small angle to that plane. Amplitude and frequency are however focussed to the polar ecliptic.
, thus multiplying the GHz frequency of the resonant cavity that accelerates the electrons into the X-ray range. The radiated power is given by the relativistic Larmor formula while the force on the emitting electron is given by the Abraham–Lorentz–Dirac force.
The radiation pattern can be distorted from an isotropic dipole pattern into an extremely forward-pointing cone of radiation. Synchrotron radiation is the brightest artificial source of X-rays.
The planar acceleration geometry appears to make the radiation linearly polarized when observed in the orbital plane, and circularly polarized when observed at a small angle to that plane. Amplitude and frequency are however focussed to the polar ecliptic.
Synchrotron radiation from accelerators
Synchrotron radiation may occur in accelerators either as a nuisance, causing undesired energy loss in particle physics contexts, or as a deliberately produced radiation source for numerous laboratory applications. Electrons are accelerated to high speeds in several stages to achieve a final energy that is typically in the GeV range. In the LHC proton bunches also produce the radiation at increasing amplitude and frequency as they accelerate with respect to the vacuum field, propagating photoelectrons, which in turn propagate secondary electrons from the pipe walls with increasing frequency and density up to 7x1010. Each proton may lose 6.7keV per turn due to this phenomenon.[3]
Synchrotron radiation in astronomy

Synchrotron radiation is also generated by astronomical objects, typically where relativistic electrons spiral (and hence change velocity) through magnetic fields. Two of its characteristics include non-thermal power-law spectra, and polarization.[4]
History of detection
It was first detected in a jet emitted by Messier 87 in 1956 by Geoffrey R. Burbidge,[5] who saw it as confirmation of a prediction by Iosif S. Shklovsky in 1953, but it had been predicted earlier by Hannes Alfvén and Nicolai Herlofson[6] in 1950.
T. K. Breus noted that questions of priority on the history of astrophysical synchrotron radiation is complicated, writing:
- "In particular, the Russian physicist V.L. Ginzburg broke his relationships with I.S. Shklovsky and did not speak with him for 18 years. In the West, Thomas Gold and Sir Fred Hoyle were in dispute with H. Alfven and N. Herlofson, while K.O. Kiepenheuer and G. Hutchinson were ignored by them."[7]

Supermassive black holes have been suggested for producing synchrotron radiation, by ejection of jets produced by gravitationally accelerating ions through the super contorted 'tubular' polar areas of magnetic fields. Such jets, the nearest being in Messier 87, have been confirmed by the Hubble telescope as apparently superluminal, travelling at 6×c (six times the speed of light) from our planetary frame. This phenomenon is caused because the jets are travelling very near the speed of light and at a very small angle towards the observer. Because at every point of their path the high-velocity jets are emitting light, the light they emit does not approach the observer much more quickly than the jet itself. Light emitted over hundreds of years of travel thus arrives at the observer over a much smaller time period (ten or twenty years) giving the illusion of faster than light travel. There is no violation of special relativity.[8]
Pulsar wind nebulae
A class of astronomical sources where synchrotron emission is important is the pulsar wind nebulae, a.k.a. plerions, of which the Crab nebula and its associated pulsar are archetypal. Pulsed emission gamma-ray radiation from the Crab has recently been observed up to ≥25 GeV,[9] probably due to synchrotron emission by electrons trapped in the strong magnetic field around the pulsar. Polarization in the Crab[10] at energies from 0.1 to 1.0 MeV illustrates a typical synchrotron radiation.
Formulation
Liénard–Wiechert Field
We start with the expressions for the Liénard–Wiechert field :
where
which is the unit vector between the observation point and the position of the charge at the retarded time, and 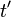 is the retarded time.
is the retarded time.
In equation (1), and (2), the first terms fall off as the inverse square of the distance from the particle, and this first term is called the generalized Coulomb field or velocity field. And the second terms fall off as the inverse first power of the distance from the source, and it is called the radiation field or acceleration field. If we ignore the velocity field, the radial component of Poynting's Vector resulted from the Liénard–Wiechert field can be calculated to be
Note that
- The spatial relationship between
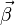 and
and 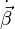 determines the detailed angular power distribution.
determines the detailed angular power distribution. - The relativistic effect of transforming from the rest frame of the particle to the observer's frame manifests itself by the presence of the factors
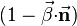 in the denominator of Eq. (3).
in the denominator of Eq. (3). - For ultrarelativistic particles the latter effect dominates the whole angular distribution.
The energy radiated into per solid angle during a finite period of acceleration from 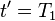 to
to 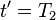 is
is
Integrating Eq. (4) over the all solid angles, we get relativistic generalization of Larmor's formula
However, this also can be derived by relativistic transformation of the 4-acceleration in Larmor's formula.
Velocity ⊥ acceleration: synchrotron radiation

When the charge is in instantaneous circular motion, its acceleration 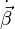 is perpendicular to its velocity
is perpendicular to its velocity 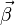 . Choosing a coordinate system such that instantaneously
. Choosing a coordinate system such that instantaneously 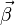 is in the z direction and
is in the z direction and 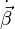 is in the x direction, with the polar and azimuth angles
is in the x direction, with the polar and azimuth angles  and
and  defining the direction of observation, the general formula Eq. (4) reduces to
defining the direction of observation, the general formula Eq. (4) reduces to
In the relativistic limit 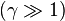 , the angular distribution can be written approximately as
, the angular distribution can be written approximately as
The factors 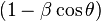 in the denominators tip the angular distribution forward into a narrow
cone like the beam of a headlight pointing ahead of the particle. A plot of the angular distribution (dP/dΩ vs. γθ) shows a sharp peak around θ=0.
in the denominators tip the angular distribution forward into a narrow
cone like the beam of a headlight pointing ahead of the particle. A plot of the angular distribution (dP/dΩ vs. γθ) shows a sharp peak around θ=0.
Integration over the whole solid angle yields the total power radiated by one electron
where E is the electron energy, B is the magnetic field, and ρ is the radius of curvature of the track in the field. Note that the radiated power is proportional to 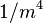 ,
, 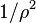 , and
, and 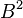 . In some cases the surfaces of vacuum chambers hit by synchrotron radiation have to be cooled because of the high power of the radiation.
. In some cases the surfaces of vacuum chambers hit by synchrotron radiation have to be cooled because of the high power of the radiation.
Using 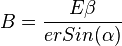 where
where  is the angle between the velocity and the magnetic field and r is the radium of the circular acceleration. The power emitted is:
is the angle between the velocity and the magnetic field and r is the radium of the circular acceleration. The power emitted is: 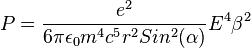 Thus the power emitted increases with the energy to the fourth and decrease with the radius to the square and the mass to the fourth. This radiation is what limit the energy of an electron-positron circular collider. For a proton-antiproton collider, the energy is limited by the maximum magnetic field, this is why the LHC has an energy only 70 times higher than the LEP even though the mass of the proton being 2000 times higher than the mass of the electron, the energy could be 2000 times higher to have the same synchroton radiation.
Thus the power emitted increases with the energy to the fourth and decrease with the radius to the square and the mass to the fourth. This radiation is what limit the energy of an electron-positron circular collider. For a proton-antiproton collider, the energy is limited by the maximum magnetic field, this is why the LHC has an energy only 70 times higher than the LEP even though the mass of the proton being 2000 times higher than the mass of the electron, the energy could be 2000 times higher to have the same synchroton radiation.
Radiation integral
The energy received by an observer (per unit solid angle at the source) is
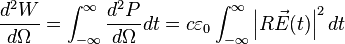
Using the Fourier Transformation we move to the frequency space
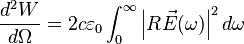
Angular and frequency distribution of the energy received by an observer (consider only the radiation field)
![\frac{d^3W}{d\Omega d\omega }=2c\varepsilon _0R^2\left | \vec{E}(\omega) \right |^2=\frac{e^2}{4\pi\varepsilon_0 4\pi^2 c}\left | \int_{-\infty}^{\infty}\frac{\hat{n}\times\left [ \left ( \hat{n}-\vec{\beta } \right )\times\dot{\vec{\beta }} \right ]}{\left ( 1-\hat{n}\cdot \vec{\beta } \right )^2}e^{i\omega(t-\hat{n}\cdot\vec{r}(t)/c)}dt\right |^2 \qquad (9)](../I/m/68d0fcb5b9d36080cac603fa5d7a93e5.png)
Therefore, if we know the particle's motion, cross products term, and phase factor, we could calculate the radiation integral. However, calculations are generally quite lengthy (even for simple cases as for the radiation emitted by an electron in a bending magnet, they require Airy function or the modified Bessel functions).
Example 1: bending magnet
Integrating
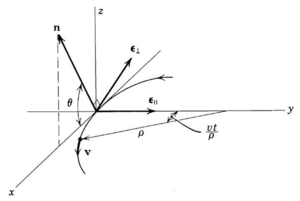
Trajectory of the arc of circumference is
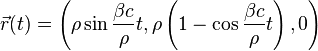
In the limit of small angles we compute
![\hat{n}\times\left ( \hat{n}\times\vec{\beta} \right )
=\beta\left [ -\vec{\varepsilon }_\parallel \sin\left ( \frac{\beta c t}{\rho} \right )+\vec{\varepsilon}_\perp \cos\left ( \frac{\beta c t}{\rho}\right )\sin\theta
\right ]](../I/m/85b78eec27ca417a6966daa06550ddd8.png)
![\omega\left ( t-\frac{\hat{n}\cdot \vec{r}(t)}{c} \right )
=
\omega\left [ t-\frac{\rho}{c}\sin\left ( \frac{\beta c t}{\rho} \right )\cos\theta \right ]](../I/m/869bedaaee66ba73cf1a5f73d229e5c6.png)
Substituting into the radiation integral and introducing 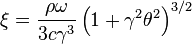
![\frac{d^3 W}{d\Omega d\omega}=\frac{e^2}{16\pi^3\varepsilon_0 c}
\left ( \frac{2\omega\rho}{3c\gamma^2} \right )^2
\left ( 1+\gamma^2 \theta^2 \right )^2
\left [ K_{2/3}^2(\xi ) + \frac{\gamma^2 \theta^2}{1+\gamma^2 \theta^2}K_{1/3}^2(\xi)\right ]\qquad (10)](../I/m/066c1b1d0d4e3d9bed32ec28a0ddbce4.png)
, where the function  is a modified Bessel function of the second kind.
is a modified Bessel function of the second kind.
Frequency distribution of radiated energy

From Eq.(10), we observe that the radiation intensity is negligible for 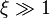 .
Critical frequency is defined as the frequency when
.
Critical frequency is defined as the frequency when 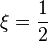 and
and  . So,
. So,
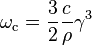 ,
,
and critical angle is defined as the angle for which 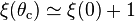 and is approximately
and is approximately
For frequencies much larger than the critical frequency and angles much larger than the critical angle, the synchrotron radiation emission is negligible.
Integrating on all angles, we get the frequency distribution of the energy radiated.

If we define
, where 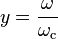 . Then,
. Then,
Note that 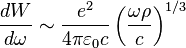 , if
, if 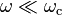 , and
, and 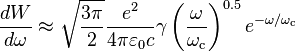 , if
, if 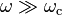
The formula for spectral distribution of synchrotron radiation, given above, can be expressed in terms of a rapidly converging integral with no special functions involved [12] (see also modified Bessel functions ) by means of the relation:
Synchrotron radiation emission as a function of the beam energy

First, define the critical photon energy as
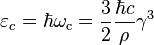
Then, the relationship between radiated power and photon energy is shown in the graph on the right side. The higher the critical energy, the more photons with high energies are generated. Note that, there is no dependence on the energy at longer wavelength.
Polarization of synchrotron radiation
In Eq.(10), the first term 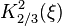 is the radiation power with polarization in the orbit plane, and the second term
is the radiation power with polarization in the orbit plane, and the second term 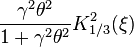 is the polarization orthogonal to the orbit plane.
In the orbit plane
is the polarization orthogonal to the orbit plane.
In the orbit plane  , the polarization is purely horizontal.
Integrating on all frequencies, we get the angular distribution of the energy radiated
, the polarization is purely horizontal.
Integrating on all frequencies, we get the angular distribution of the energy radiated
Integrating on all the angles, we find that seven times as much energy is radiated with parallel polarization as with perpendicular polarization. The radiation from a relativistically moving charge is very strongly, but not completely, polarized in the plane of motion.
Example 2: undulator
Solution of equation of motion and undulator equation
An undulator consists of a periodic array of magnets, so that they provide a sinusoidal magnetic field.

Solution of equation of motion is
where,
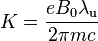 , and
, and
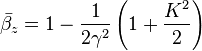
, and the parameter  is called the undulator parameter.
is called the undulator parameter.

Condition for the constructive interference of radiation emitted at different poles is
Expanding 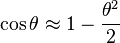 and neglecting the terms
and neglecting the terms 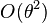 in the resulting equation, one obtains
in the resulting equation, one obtains
For  one finally gets
one finally gets
This equation is called the undulator equation.
Radiation from the undulator
Radiation integral is
Using the periodicity of the trajectory, we can split the radiation integral into a sum over 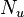 terms.
terms.
, where 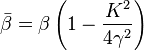

, and
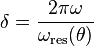 ,
, 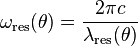 , and
, and 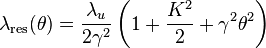


The radiation integral in an undulator can be written as
The sum of 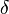 generates a series of sharp peaks in the frequency spectrum harmonics of fundamental wavelength
generates a series of sharp peaks in the frequency spectrum harmonics of fundamental wavelength
, and  depends on the angles of observations and
depends on the angles of observations and 
On the axis( ,
,  ), the radiation integral becomes
), the radiation integral becomes
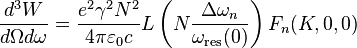
and,
![F_n(K,0,0)=\frac{n^2K^2}{1+K^2/2}
\left[J_{\frac{n+1}{2}}(Z)-J_{\frac{n-1}{2}}(Z) \right ]^2](../I/m/8c9414bc5baea582a59de6d072af1ce6.png)
, where 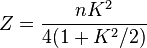
Note that only odd harmonics are radiated on-axis, and as K increases higher harmonic becomes stronger.
See also
- Bremsstrahlung
- Cyclotron turnover
- Free-electron laser
- Radiation reaction
- Relativistic beaming
- Sokolov–Ternov effect
Notes
- ↑ Elder, F. R.; Gurewitsch, A. M.; Langmuir, R. V.; Pollock, H. C., "Radiation from Electrons in a Synchrotron" (1947) Physical Review, vol. 71, Issue 11, pp. 829-830
- ↑ Iwanenko D., Pomeranchuk I., "On the maximal energy attainable in betatron", (1944) Physical Review vol.65, p. 343
- ↑ Synchrotron Radiation Damping in the LHC 2005 Joachim Tuckmantel.
- ↑ Vladimir A. Bordovitsyn, "Synchrotron Radiation in Astrophysics" (1999) Synchrotron Radiation Theory and Its Development, ISBN 981-02-3156-3
- ↑ Burbidge, G. R. "On Synchrotron Radiation from Messier 87. Astrophysical Journal, vol. 124, p. 416"
- ↑ Alfvén, H.; Herlofson, N. "Cosmic Radiation and Radio Stars" Physical Review (1950), vol. 78, Issue 5, pp. 616–616
- ↑ Breus, T. K., "Istoriya prioritetov sinkhrotronnoj kontseptsii v astronomii %t (Historical problems of the priority questions of the synchrotron concept in astrophysics)" (2001) in Istoriko-Astronomicheskie Issledovaniya, Vyp. 26, p. 88 - 97, 262 (2001)
- ↑ Chase, Scott I. "Apparent Superluminal Velocity of Galaxies". Retrieved 22 August 2012.
- ↑ "Observation of Pulsed {gamma}-Rays Above 25 GeV from the Crab Pulsar with MAGIC", Science 21 November 2008: Vol. 322. no. 5905, pp. 1221–1224"
- ↑ Dean et al.,"Polarized Gamma-Ray Emission from the Crab", Science 29 August 2008: Vol. 321. no. 5893, pp. 1183–1185
- ↑ Jackson, John David (1999). Classical Electrodynamics (3rd ed.). Chichester: Wiley. p. 680. ISBN 0-471-30932-X.
- ↑ M.Kh.Khokonov. Cascade Processes of Energy Loss by Emission of Hard Photons // JETP, V.99, No.4, pp. 690-707 \ (2004).
References
- Brau, Charles A. Modern Problems in Classical Electrodynamics. Oxford University Press, 2004. ISBN 0-19-514665-4.
- Jackson, John David. Classical Electrodynamics. John Wiley & Sons, 1999. ISBN 0-471-30932-X
- Ishfaq Ahmad, D.Sc. "Measurements of the Relative Oscillator Strengths using the Synchrotron Radiation" (PDF). Proceedings of the National Syposium on Frontier of Physics, National Centre for Theoretical Physics. Pakistan Physical Society. Retrieved 16 January 2012.
External links
- Cosmic Magnetobremsstrahlung (synchrotron Radiation), by Ginzburg, V. L., Syrovatskii, S. I., ARAA, 1965
- Developments in the Theory of Synchrotron Radiation and its Reabsorption, by Ginzburg, V. L., Syrovatskii, S. I., ARAA, 1969
- Lightsources.org
- X-Ray Data Booklet
![\mathbf{B}(\mathbf{r},t)=-\frac{\mu_0q}{4\pi}\left[\frac{c\,\hat{\mathbf{n}}\times\vec{\beta}}{\gamma^2R^2(1-\vec{\beta}\mathbf{\cdot}\hat{\mathbf{n}})^3}+\frac{\hat{\mathbf{n}}\times[\,\dot{\vec{\beta}}+\hat{\mathbf{n}}\times(\vec{\beta}\times\dot{\vec{\beta}})]}{R\,(1-\vec{\beta}\mathbf{\cdot}\hat{\mathbf{n}})^3}\right]_{\mathrm{retarded}} \qquad (1)](../I/m/fdad937b33e33dc00caa6a8b75173632.png)
![\mathbf{E}(\mathbf{r},t)=\frac{q}{4\pi\varepsilon_0}\left[\frac{\hat{\mathbf{n}}-\vec{\beta}}{\gamma^2R^2(1-\vec{\beta}\mathbf{\cdot}\hat{\mathbf{n}})^3}+\frac{\hat{\mathbf{n}}\times[(\hat{\mathbf{n}}-\vec{\beta})\times\dot{\vec{\beta}}\,]}{c\,R\,(1-\vec{\beta}\mathbf{\cdot}\hat{\mathbf{n}})^3}\right]_{\mathrm{retarded}} \qquad \qquad (2)](../I/m/be45a49c5a90f9039143b9e95bbdc152.png)
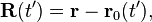
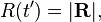
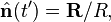
![[\mathbf{S\cdot}\hat{\mathbf{n}}] = \frac{q^2}{16\pi^2\varepsilon_0 c}\left\{\frac{1}{R^2}\left|\frac{\hat{\mathbf{n}}\times[(\hat{\mathbf{n}}-\vec{\beta})\times\dot{\vec{\beta}}]}{(1-\vec{\beta}\mathbf{\cdot}\hat{\mathbf{n}})^3}\right|^2\right\}_{\text{retarded}} \qquad \qquad (3)](../I/m/36c87887aef0a78b6d6ba8e9531bddaf.png)
![\frac{\mathrm{d}P}{\mathrm{d}\mathit{\Omega}} = R(t')^2\,[\mathbf{S}(t')\mathbf{\cdot}\hat{\mathbf{n}}(t')]\,\frac{\mathrm{d}t}{\mathrm{d}t'} = R(t')^2\,\mathbf{S}(t')\mathbf{\cdot}\hat{\mathbf{n}}(t')\,[1-\vec{\beta}(t')\mathbf{\cdot}\hat{\mathbf{n}}(t')]](../I/m/c4667c96539229c14cb8ede008421932.png)
![= \frac{q^2}{16\pi^2\varepsilon_0c}\,\frac{|\hat{\mathbf{n}}(t')\times\{[\hat{\mathbf{n}}(t')-\vec{\beta}(t')]\times\dot{\vec{\beta}}(t')\}|^2}{[1-\vec{\beta}(t')\mathbf{\cdot}\vec{\mathbf{n}}(t')]^5} \qquad \qquad (4)](../I/m/49622442da458aa4de83cdfed161e68f.png)
![P=\frac{e^2}{6\pi \varepsilon _0 c}\gamma ^6
\left [ \left | \dot{\vec{\beta }} \right |^2
-\left | \vec{\beta}\times \dot{\vec{\beta }}\right |^2 \right ]\qquad (5)](../I/m/68142df8de3c4ff5a78dc3a3153cc400.png)
![\frac{\mathrm{d}P}{\mathrm{d}\mathit{\Omega}} = \frac{q^2}{16\pi^2\epsilon_0 c}\frac{|\dot{\vec{\beta }}|^2}{(1-\beta\cos\theta)^3}\left[1-\frac{\sin^2\theta\cos^2\phi}{\gamma^2(1-\beta\cos\theta)^2}\right]. \qquad (6)](../I/m/fcbbb33e0cacfc01441a70608753c0a0.png)
![\frac{\mathrm{d}P}{\mathrm{d}\mathit{\Omega}} \simeq \frac{2}{\pi}\frac{e^2}{c^3}\gamma^6\frac{|\dot{\mathbf v}|^2}{(1+\gamma^2\theta^2)^3}\left[1-\frac{4\gamma^2\theta^2\cos^2\phi}{(1+\gamma^2\theta^2)^2}\right]. \qquad \qquad (7)](../I/m/7bb249908faeeed6ea5e57de7f428df5.png)
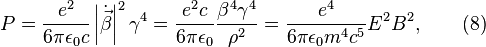
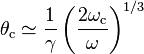
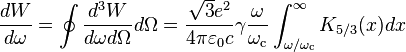
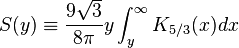
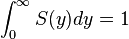
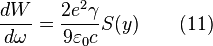
![\int_{\xi}^\infty K_{5/3} (x) dx = \frac{1}{ \sqrt{3}} \, \int_0^\infty \, \frac{9+36x^2+16x^4}{(3+4x^2) \sqrt{1+x^2/3}}
\exp \left[- \xi \left(1+\frac{4x^2}{3}\right) \sqrt{1+\frac{x^2}{3}} \right] \ dx](../I/m/711492f1074c93a4e3a880a55eef8a1d.png)
![\frac{d^2 W}{d\Omega }=\int_{0}^{\infty}\frac{d^3W}{d\omega d\Omega }d\omega
=\frac{7e^2 \gamma^5}{64\pi\varepsilon_0\rho}\frac{1}{(1+\gamma^2\theta^2)^{5/2}}\left [1+\frac{5}{7}\frac{\gamma^2\theta^2}{1+\gamma^2\theta^2} \right ] \qquad (12)](../I/m/3be0abb41e3260d3bf98010d00ca1150.png)
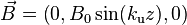
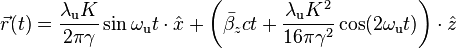
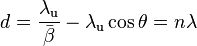
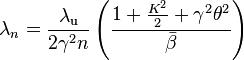
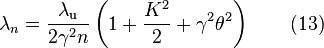
![\frac{d^3W}{d\Omega d\omega}=\frac{e^2}{4\pi\varepsilon_0 4\pi^2 c}\left|\int_{-\infty}^{\infty}\frac{\hat{n}\times\left[\left(\hat{n}-\vec{\beta}\right)\times\dot{\vec{\beta}}\right]}{\left(1-\hat{n}\cdot\vec{\beta}\right)^2}e^{i\omega(t-\hat{n}\cdot\vec{r}(t)/c)}dt\right|^2](../I/m/ac95b4ae2d2b807a595232647f972002.png)