Symmetric monoidal category
In category theory, a branch of mathematics, a symmetric monoidal category is a braided monoidal category that is maximally symmetric. That is, the braiding operator 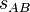 obeys an additional identity:
obeys an additional identity: 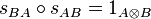 .
.
The classifying space (geometric realization of the nerve) of a symmetric monoidal category is an  space, so its group completion is an infinite loop space.[1]
space, so its group completion is an infinite loop space.[1]
Definition
A symmetric monoidal category is a monoidal category (C, ⊗) such that, for every pair A, B of objects in C, there is an isomorphism 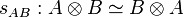 that is natural in both A and B and such that the following diagrams commute:
that is natural in both A and B and such that the following diagrams commute:
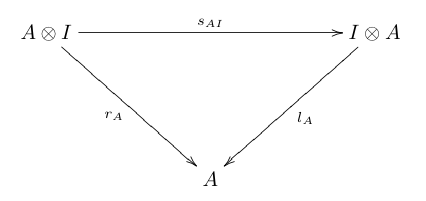
- The unit coherence:
- The associativity coherence:
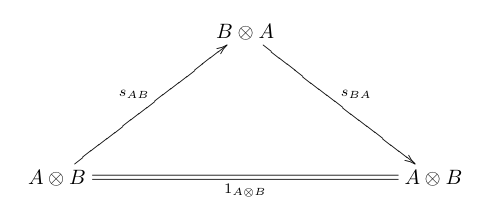
- The inverse law:
In the diagrams above, a, l , r are the associativity isomorphism, the left unit isomorphism, and the right unit isomorphism respectively.
Examples
The prototypical example is the category of vector spaces. Some examples and non-examples of symmetric monoidal categories:
- The category of sets. The tensor product is the set theoretic cartesian product, and any singleton can be fixed as the unit object.
- The category of groups. Like before, the tensor product is just the cartesian product of groups, and the trivial group is the unit object.
- More generally, a category with finite products, that is, a Cartesian monoidal category, is symmetric monoidal. The tensor product is the direct product of objects, and any terminal object (empty product) is the unit object.
- The category of bimodules over a ring R is monoidal, but not necessarily symmetric. If R is commutative, the category of left R-modules is symmetric monoidal.
- The dagger symmetric monoidal categories are symmetric monodal categories with an additional dagger structure.
A cosmos is a complete cocomplete closed symmetric monoidal category.
References
- ↑ R.W. Thomason, "Symmetric Monoidal Categories Model all Connective Spectra", Theory and Applications of Categories, Vol. 1, No. 5, 1995, pp. 78– 118.
- Symmetric monoidal category in nLab
- This article incorporates material from Symmetric monoidal category on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.