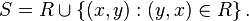Symmetric closure
In mathematics, the symmetric closure of a binary relation R on a set X is the smallest symmetric relation on X that contains R.
For example, if X is a set of airports and xRy means "there is a direct flight from airport x to airport y", then the symmetric closure of R is the relation "there is a direct flight either from x to y or from y to x". Or, if X is the set of humans (alive or dead) and R is the relation 'parent of', then the symmetric closure of R is the relation "x is a parent or a child of y".
Definition
The symmetric closure S of a relation R on a set X is given by
In other words, the symmetric closure of R is the union of R with its inverse relation, R -1.
See also
References
- Franz Baader and Tobias Nipkow, Term Rewriting and All That, Cambridge University Press, 1998, p. 8
This article is issued from Wikipedia - version of the Thursday, September 25, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.