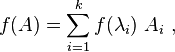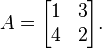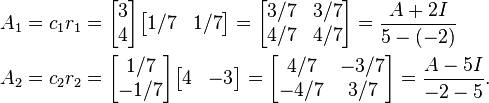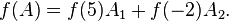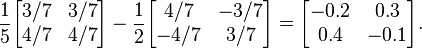Sylvester's formula

In matrix theory, Sylvester's formula or Sylvester's matrix theorem (named after J. J. Sylvester) or Lagrange−Sylvester interpolation expresses an analytic function $f (A)$ of a matrix $A$ as a polynomial in $A$ , in terms of the eigenvalues and eigenvectors of $A$ .^[1]^[2] It states that

f(A) = \sum_{i=1}^k f(\lambda_i) ~ A_i ~,

where the $λ i$ are the eigenvalues of $A$ , and the matrices $A$ _i are the corresponding Frobenius covariants of $A$ , which are (projection) matrix Lagrange polynomials of $A$ .

Sylvester's formula (1883) is only valid for diagonalizable matrices; an extension due to A. Buchheim (1886) covers the general case.

Conditions

Sylvester's formula applies for any diagonalizable matrix $A$ with $k$ distinct eigenvalues, $λ$ ₁, …, λ_k, and any function $f$ defined on some subset of the complex numbers such that $f (A)$ is well defined. The last condition means that every eigenvalue $λ i$ is in the domain of $f$ , and that every eigenvalue $λ i$ with multiplicity $m$ _i > 1 is in the interior of the domain, with $f$ being ( $m i — 1$ ) times differentiable at $λ i$ .^[1]^:Def.6.4

Example

Consider the two-by-two matrix:

A = \begin{bmatrix} 1 & 3 \\ 4 & 2 \end{bmatrix}.

This matrix has two eigenvalues, 5 and −2. Its Frobenius covariants are

\begin{align} A_1 &= c_1 r_1 = \begin{bmatrix} 3 \\ 4 \end{bmatrix} \begin{bmatrix} 1/7 & 1/7 \end{bmatrix} = \begin{bmatrix} 3/7 & 3/7 \\ 4/7 & 4/7 \end{bmatrix} = \frac{A+2I}{5-(-2)}\\ A_2 &= c_2 r_2 = \begin{bmatrix} 1/7 \\ -1/7 \end{bmatrix} \begin{bmatrix} 4 & -3 \end{bmatrix} = \begin{bmatrix} 4/7 & -3/7 \\ -4/7 & 3/7 \end{bmatrix}=\frac{A-5I}{-2-5}. \end{align}

Sylvester's formula then amounts to

f(A) = f(5) A_1 + f(-2) A_2. \,

For instance, if $f$ is defined by $f (x) = x -1$ , then Sylvester's formula expresses the matrix inverse $f (A) = A -1$ as

\frac{1}{5} \begin{bmatrix} 3/7 & 3/7 \\ 4/7 & 4/7 \end{bmatrix} - \frac{1}{2} \begin{bmatrix} 4/7 & -3/7 \\ -4/7 & 3/7 \end{bmatrix} = \begin{bmatrix} -0.2 & 0.3 \\ 0.4 & -0.1 \end{bmatrix}.

References

1 2 Roger A. Horn and Charles R. Johnson (1991), Topics in Matrix Analysis. Cambridge University Press, ISBN 978-0-521-46713-1
↑ Jon F. Claerbout (1976), Sylvester's matrix theorem, a section of Fundamentals of Geophysical Data Processing. Online version at sepwww.stanford.edu, accessed on 2010-03-14.

F.R. Gantmacher, The Theory of Matrices v I (Chelsea Publishing, NY, 1960) ISBN 0-8218-1376-5 , pp 101-103

This article is issued from Wikipedia - version of the Thursday, February 04, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.