Susskind–Glogower operator

The Susskind–Glogower operator, first proposed by Leonard Susskind and J. Glogower,[1] refers to the operator where the phase is introduced as an approximate polar decomposition of the creation and annihilation operators.

It is defined as

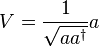V=\frac{1}{\sqrt{aa^{\dagger}}}a,

and its adjoint

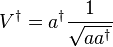V^{\dagger}=a^{\dagger}\frac{1}{\sqrt{aa^{\dagger}}}.

Their commutation relation is

[V,V^{\dagger}]=|0\rangle\langle 0|,

where |0\rangle is the vacuum state of the harmonic oscillator.

They may be regarded as a (exponential of) phase operator because

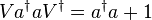Va^{\dagger}a V^{\dagger}=a^{\dagger}a+1,

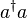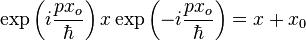where a^{\dagger}a is the number operator. So the exponential of the phase operator displaces the number operator in the same fashion as \exp\left(i\frac{px_o}{\hbar}\right)x\exp\left(-i\frac{px_o}{\hbar}\right)=x+x_0.

They may be used to solve problems such as atom-field interactions,[2] level-crossings [3] or to define some class of non-linear coherent states,[4] among others.

References

  1. ↑ L. Susskind and J. Glogower, Physica 1, 49 (1964)
  2. ↑ B. M. Rodríguez-Lara and H.M. Moya-Cessa, Journal of Physics A 46, 095301 (2013). Exact solution of generalized Dicke models via Susskind-Glogower operators http://dx.doi.org/10.1088/1751-8113/46/9/095301.
  3. ↑ B.M. Rodríguez-Lara, D. Rodríguez-Méndez and H. Moya-Cessa, Physics Letters A 375, 3770-3774 (2011). Solution to the Landau-Zener problem via Susskind-Glogower operators. http://dx.doi.org/10.1016/j.physleta.2011.08.051
  4. ↑ R. de J. León-Montiel, H. Moya-Cessa, F. Soto-Eguibar, Revista Mexicana de Física S 57, 133 (2011). Nonlinear coherent states for the Susskind-Glogower operators. http://rmf.smf.mx/pdf/rmf-s/57/3/57_3_133.pdf
This article is issued from Wikipedia - version of the Saturday, August 09, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.