Suspension of a ring

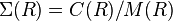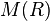In algebra, more specifically in algebraic K-theory, the suspension $\Sigma R$ of a ring R is given by^[1] $\Sigma(R) = C(R)/M(R)$ where $C(R)$ is the ring of all infinite matrices with coefficients in R having only finitely many nonzero elements in each row or column and $M(R)$ is its ideal of matrices having only finitely many nonzero elements. It is an analog of suspension in topology.

One then has: 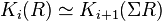$K_i(R) \simeq K_{i+1}(\Sigma R)$ .

References

↑ Weibel, III, Ex. 1.15

C. Weibel "The K-book: An introduction to algebraic K-theory"

This article is issued from Wikipedia - version of the Tuesday, December 10, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.