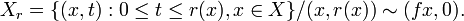Suspension (dynamical systems)

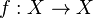Suspension is a construction passing from a map to a flow. Namely, let $X$ be a metric space, $f:X\to X$ be a continuous map and 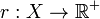$r:X\to\mathbb{R}^+$ be a function (roof function or ceiling function) bounded away from 0. Consider the quotient space

X_r=\{(x,t):0\le t\le r(x),x\in X\}/(x,r(x))\sim(fx,0).

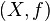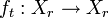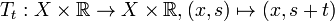The suspension of $(X,f)$ with roof function $r$ is the semiflow^[1] $f_t:X_r\to X_r$ induced by the time-translation $T_t:X\times\mathbb{R}\to X\times\mathbb{R}, (x,s)\mapsto (x,s+t)$ .

If 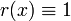$r(x)\equiv 1$ , then the quotient space is also called the mapping torus of $(X,f)$ .

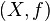References

↑ M. Brin and G. Stuck, Introduction to Dynamical Systems, Cambridge University Press, 2002.

This article is issued from Wikipedia - version of the Wednesday, January 09, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.