Supersymmetry

"SUSY" redirects here. For other uses, see Susy (disambiguation).
For the episode of the American TV series Angel, see Supersymmetry (Angel).

In particle physics, Supersymmetry (SUSY) is a proposed type of spacetime symmetry that relates two basic classes of elementary particles: bosons, which have an integer-valued spin, and fermions, which have a half-integer spin.[1] Each particle from one group is associated with a particle from the other, known as its superpartner, the spin of which differs by a half-integer. In a theory with perfectly "unbroken" supersymmetry, each pair of superpartners would share the same mass and internal quantum numbers besides spin. For example, there would be a "selectron" (superpartner electron), a bosonic version of the electron with the same mass as the electron, that would be easy to find in a laboratory. Thus, since no superpartners have been observed, if supersymmetry exists it must be a spontaneously broken symmetry so that superpartners may differ in mass.[2][3] Spontaneously-broken supersymmetry could solve many mysterious problems in particle physics including the hierarchy problem. The simplest realization of spontaneously-broken supersymmetry, the so-called Minimal Supersymmetric Standard Model, is one of the best studied candidates for physics beyond the Standard Model.

There is only indirect evidence and motivation for the existence of supersymmetry. Direct confirmation would entail production of superpartners in collider experiments, such as the Large Hadron Collider (LHC). The first run of the LHC found no evidence for supersymmetry (all results were consistent with the Standard Model), and thus set limits on superpartner masses in supersymmetric theories. While many remain enthusiastic about supersymmetry,[4] this first run at the LHC led some physicists to explore other ideas.[5] The LHC resumed its search for supersymmetry and other new physics in its second run.

Motivations

There are numerous phenomenological motivations for supersymmetry close to the electroweak scale, as well as technical motivations for supersymmetry at any scale.

The hierarchy problem

Supersymmetry close to the electroweak scale ameliorates the hierarchy problem that afflicts the Standard Model. In the Standard Model, the electroweak scale receives enormous Planck-scale quantum corrections. The observed hierarchy between the electroweak scale and the Planck scale must be achieved with extraordinary fine tuning. In a supersymmetric theory, on the other hand, Planck-scale quantum corrections cancel between partners and superpartners (owing to a minus sign associated with fermionic loops). The hierarchy between the electroweak scale and the Planck scale is achieved in a natural manner, without miraculous fine-tuning.

Gauge coupling unification

The idea that the gauge symmetry groups unify at high-energy is called Grand unification theory. In the Standard Model, however, the weak, strong and electromagnetic couplings fail to unify at high energy. In a supersymmetry theory, the running of the gauge couplings are modified, and precise high-energy unification of the gauge couplings is achieved. The modified running also provides a natural mechanism for radiative electroweak symmetry breaking.

Dark matter

TeV-scale supersymmetry (augmented with a discrete symmetry) typically provides a candidate dark matter particle at a mass scale consistent with thermal relic abundance calculations.[6][7]

Other technical motivations

Supersymmetry is also motivated by solutions to several theoretical problems, for generally providing many desirable mathematical properties, and for ensuring sensible behavior at high energies. Supersymmetric quantum field theory is often much easier to analyze, as many more problems become exactly solvable. When supersymmetry is imposed as a local symmetry, Einstein's theory of general relativity is included automatically, and the result is said to be a theory of supergravity. It is also a necessary feature of the most popular candidate for a theory of everything, superstring theory.

Another theoretically appealing property of supersymmetry is that it offers the only "loophole" to the Coleman–Mandula theorem, which prohibits spacetime and internal symmetries from being combined in any nontrivial way, for quantum field theories like the Standard Model with very general assumptions. The Haag-Lopuszanski-Sohnius theorem demonstrates that supersymmetry is the only way spacetime and internal symmetries can be combined consistently.[8]

History

A supersymmetry relating mesons and baryons was first proposed, in the context of hadronic physics, by Hironari Miyazawa during 1966. This supersymmetry did not involve spacetime, that is, it concerned internal symmetry, and was broken badly. Miyazawa's work was largely ignored at the time.[9][10][11][12]

J. L. Gervais and B. Sakita (during 1971),[13] Yu. A. Golfand and E. P. Likhtman (also during 1971), and D.V. Volkov and V.P. Akulov (1972),[14] independently rediscovered supersymmetry in the context of quantum field theory, a radically new type of symmetry of spacetime and fundamental fields, which establishes a relationship between elementary particles of different quantum nature, bosons and fermions, and unifies spacetime and internal symmetries of microscopic phenomena. Supersymmetry with a consistent Lie-algebraic graded structure on which the Gervais−Sakita rediscovery was based directly first arose during 1971[15] in the context of an early version of string theory by Pierre Ramond, John H. Schwarz and André Neveu.

Finally, Julius Wess and Bruno Zumino (during 1974)[16] identified the characteristic renormalization features of four-dimensional supersymmetric field theories, which identified them as remarkable QFTs, and they and Abdus Salam and their fellow researchers introduced early particle physics applications. The mathematical structure of supersymmetry (Graded Lie superalgebras) has subsequently been applied successfully to other topics of physics, ranging from nuclear physics,[17][18] critical phenomena,[19] quantum mechanics to statistical physics. It remains a vital part of many proposed theories of physics.

The first realistic supersymmetric version of the Standard Model was proposed during 1977 by Pierre Fayet and is known as the Minimal Supersymmetric Standard Model or MSSM for short. It was proposed to solve, amongst other things, the hierarchy problem.

Applications

Extension of possible symmetry groups

One reason that physicists explored supersymmetry is because it offers an extension to the more familiar symmetries of quantum field theory. These symmetries are grouped into the Poincaré group and internal symmetries and the Coleman–Mandula theorem showed that under certain assumptions, the symmetries of the S-matrix must be a direct product of the Poincaré group with a compact internal symmetry group or if there is not any mass gap, the conformal group with a compact internal symmetry group. During 1971 Golfand and Likhtman were the first to show that the Poincaré algebra can be extended through introduction of four anticommuting spinor generators (in four dimensions), which later became known as supercharges. During 1975 the Haag-Lopuszanski-Sohnius theorem analyzed all possible superalgebras in the general form, including those with an extended number of the supergenerators and central charges. This extended super-Poincaré algebra paved the way for obtaining a very large and important class of supersymmetric field theories.

The supersymmetry algebra

Main article: Supersymmetry algebra

Traditional symmetries of physics are generated by objects that transform by the tensor representations of the Poincaré group and internal symmetries. Supersymmetries, however, are generated by objects that transform by the spinor representations. According to the spin-statistics theorem, bosonic fields commute while fermionic fields anticommute. Combining the two kinds of fields into a single algebra requires the introduction of a Z2-grading under which the bosons are the even elements and the fermions are the odd elements. Such an algebra is called a Lie superalgebra.

The simplest supersymmetric extension of the Poincaré algebra is the Super-Poincaré algebra. Expressed in terms of two Weyl spinors, has the following anti-commutation relation:

\{ Q_{ \alpha }, \bar{Q_{ \dot{ \beta }}} \} = 2( \sigma{}^{\mu} )_{ \alpha \dot{ \beta }} P_{\mu}

and all other anti-commutation relations between the Qs and commutation relations between the Qs and Ps vanish. In the above expression 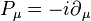P_{\mu} = -i \partial{}_{\mu} are the generators of translation and 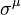\sigma{}^{\mu} are the Pauli matrices.

There are representations of a Lie superalgebra that are analogous to representations of a Lie algebra. Each Lie algebra has an associated Lie group and a Lie superalgebra can sometimes be extended into representations of a Lie supergroup.

The Supersymmetric Standard Model

Incorporating supersymmetry into the Standard Model requires doubling the number of particles since there is no way that any of the particles in the Standard Model can be superpartners of each other. With the addition of new particles, there are many possible new interactions. The simplest possible supersymmetric model consistent with the Standard Model is the Minimal Supersymmetric Standard Model (MSSM) which can include the necessary additional new particles that are able to be superpartners of those in the Standard Model.

Cancellation of the Higgs boson quadratic mass renormalization between fermionic top quark loop and scalar stop squark tadpole Feynman diagrams in a supersymmetric extension of the Standard Model

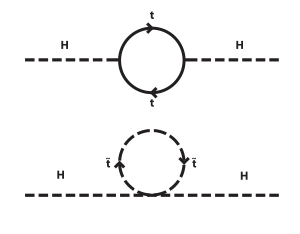
One of the main motivations for SUSY comes from the quadratically divergent contributions to the Higgs mass squared. The quantum mechanical interactions of the Higgs boson causes a large renormalization of the Higgs mass and unless there is an accidental cancellation, the natural size of the Higgs mass is the greatest scale possible. This problem is known as the hierarchy problem. Supersymmetry reduces the size of the quantum corrections by having automatic cancellations between fermionic and bosonic Higgs interactions. If supersymmetry is restored at the weak scale, then the Higgs mass is related to supersymmetry breaking which can be induced from small non-perturbative effects explaining the vastly different scales in the weak interactions and gravitational interactions.

In many supersymmetric Standard Models there is a heavy stable particle (such as neutralino) which could serve as a weakly interacting massive particle (WIMP) dark matter candidate. The existence of a supersymmetric dark matter candidate is related closely to R-parity.

The standard paradigm for incorporating supersymmetry into a realistic theory is to have the underlying dynamics of the theory be supersymmetric, but the ground state of the theory does not respect the symmetry and supersymmetry is broken spontaneously. The supersymmetry break can not be done permanently by the particles of the MSSM as they currently appear. This means that there is a new sector of the theory that is responsible for the breaking. The only constraint on this new sector is that it must break supersymmetry permanently and must give superparticles TeV scale masses. There are many models that can do this and most of their details do not matter. In order to parameterize the relevant features of supersymmetry breaking, arbitrary soft SUSY breaking terms are added to the theory which temporarily break SUSY explicitly but could never arise from a complete theory of supersymmetry breaking.

Gauge-coupling unification

One piece of evidence for supersymmetry existing is gauge coupling unification. The renormalization group evolution of the three gauge coupling constants of the Standard Model is somewhat sensitive to the present particle content of the theory. These coupling constants do not quite meet together at a common energy scale if we run the renormalization group using the Standard Model.[20] With the addition of minimal SUSY joint convergence of the coupling constants is projected at approximately 1016 GeV.[20]

Supersymmetric quantum mechanics

Supersymmetric quantum mechanics adds the SUSY superalgebra to quantum mechanics as opposed to quantum field theory. Supersymmetric quantum mechanics often becomes relevant when studying the dynamics of supersymmetric solitons, and due to the simplified nature of having fields which are only functions of time (rather than space-time), a great deal of progress has been made in this subject and it is now studied in its own right.

SUSY quantum mechanics involves pairs of Hamiltonians which share a particular mathematical relationship, which are called partner Hamiltonians. (The potential energy terms which occur in the Hamiltonians are then known as partner potentials.) An introductory theorem shows that for every eigenstate of one Hamiltonian, its partner Hamiltonian has a corresponding eigenstate with the same energy. This fact can be exploited to deduce many properties of the eigenstate spectrum. It is analogous to the original description of SUSY, which referred to bosons and fermions. We can imagine a "bosonic Hamiltonian", whose eigenstates are the various bosons of our theory. The SUSY partner of this Hamiltonian would be "fermionic", and its eigenstates would be the theory's fermions. Each boson would have a fermionic partner of equal energy.

Supersymmetry: Applications to condensed matter physics

SUSY concepts have provided useful extensions to the WKB approximation. Additionally, SUSY has been applied to disorder averaged systems both quantum and non-quantum (through statistical mechanics), the Fokker-Planck equation being an example of a non-quantum theory. The 'supersymmetry' in all these systems arises from the fact that one is modelling one particle and as such the 'statistics' don't matter. The use of the supersymmetry method provides a mathematical rigorous alternative to the replica trick, but only in non-interacting systems, which attempts to address the so-called 'problem of the denominator' under disorder averaging. For more on the applications of supersymmetry in condensed matter physics see the book[21]

Supersymmetry in optics

Integrated optics was recently found[22] to provide a fertile ground on which certain ramifications of SUSY can be explored in readily-accessible laboratory settings. Making use of the analogous mathematical structure of the quantum-mechanical Schrödinger equation and the wave equation governing the evolution of light in one-dimensional settings, one may interpret the refractive index distribution of a structure as a potential landscape in which optical wave packets propagate. In this manner, a new class of functional optical structures with possible applications in phase matching, mode conversion[23] and space-division multiplexing becomes possible. SUSY transformations have been also proposed as a way to address inverse scattering problems in optics and as a one-dimensional transformation optics [24]

Mathematics

SUSY is also sometimes studied mathematically for its intrinsic properties. This is because it describes complex fields satisfying a property known as holomorphy, which allows holomorphic quantities to be exactly computed. This makes supersymmetric models useful "toy models" of more realistic theories. A prime example of this has been the demonstration of S-duality in four-dimensional gauge theories[25] that interchanges particles and monopoles.

The proof of the Atiyah-Singer index theorem is much simplified by the use of supersymmetric quantum mechanics.

General supersymmetry

Supersymmetry appears in many related contexts of theoretical physics. It is possible to have multiple supersymmetries and also have supersymmetric extra dimensions.

Extended supersymmetry

It is possible to have more than one kind of supersymmetry transformation. Theories with more than one supersymmetry transformation are known as extended supersymmetric theories. The more supersymmetry a theory has, the more constrained are the field content and interactions. Typically the number of copies of a supersymmetry is a power of 2, i.e. 1, 2, 4, 8. In four dimensions, a spinor has four degrees of freedom and thus the minimal number of supersymmetry generators is four in four dimensions and having eight copies of supersymmetry means that there are 32 supersymmetry generators.

The maximal number of supersymmetry generators possible is 32. Theories with more than 32 supersymmetry generators automatically have massless fields with spin greater than 2. It is not known how to make massless fields with spin greater than two interact, so the maximal number of supersymmetry generators considered is 32. This is due to the Weinberg-Witten theorem. This corresponds to an N = 8 supersymmetry theory. Theories with 32 supersymmetries automatically have a graviton.

For four dimensions there are the following theories, with the corresponding multiplets[26](CPT adds a copy, whenever they are not invariant under such symmetry)

Chiral multiplet: (0,1⁄2) Vector multiplet: (1⁄2,1) Gravitino multiplet: (1,3⁄2) Graviton multiplet: (3⁄2,2)

hypermultiplet: (-1⁄2,02,1⁄2) vector multiplet: (0,1⁄22,1) supergravity multiplet: (1,3⁄22,2)

Vector multiplet: (-1,-1⁄24,06,1⁄24,1) Supergravity multiplet: (0,1⁄24,16,3⁄24,2)

Supergravity multiplet: (-2,-3⁄28,-128,-1⁄256,070,1⁄256,128,3⁄28,2)

Supersymmetry in alternate numbers of dimensions

It is possible to have supersymmetry in dimensions other than four. Because the properties of spinors change drastically between different dimensions, each dimension has its characteristic. In d dimensions, the size of spinors is approximately 2d/2 or 2(d − 1)/2. Since the maximum number of supersymmetries is 32, the greatest number of dimensions in which a supersymmetric theory can exist is eleven.

Supersymmetry in quantum gravity

Supersymmetry is part of a larger enterprise of theoretical physics to unify everything we know about the universe into a single consistent set of physical principles, known as the quest for a Theory of Everything (TOE). A significant part of this larger enterprise is the quest for a theory of quantum gravity, which would unify the classical theory of general relativity and the Standard Model, which explains the other three basic forces in physics (electromagnetism, the strong interaction, and the weak interaction), and provides a palette of fundamental particles upon which all four forces act. Two of the most active methods of forming a theory of quantum gravity are string theory and loop quantum gravity (LQG), although in theory, supersymmetry could be a component of other theories as well.

For string theory to be consistent, supersymmetry seems to be required at some level (although it may be a strongly broken symmetry). In particle theory, supersymmetry is recognized as a way to stabilize the hierarchy between the unification scale and the electroweak scale (or the Higgs boson mass), and can also provide a natural dark matter candidate. String theory also requires extra spatial dimensions which have to be compactified as in Kaluza–Klein theory.

Loop quantum gravity (LQG) predicts no additional spatial dimensions, nor anything else about particle physics. These theories can be formulated in three spatial dimensions and one dimension of time, although in some LQG theories dimensionality is an emergent property of the theory, rather than a fundamental assumption of the theory. Also, LQG is a theory of quantum gravity which does not require supersymmetry. Lee Smolin, one of the originators of LQG, has proposed that a loop quantum gravity theory incorporating either supersymmetry or extra dimensions, or both, be called "loop quantum gravity II".

If experimental evidence confirms supersymmetry in the form of supersymmetric particles such as the neutralino that is often believed to be the lightest superpartner, some people believe this would be a major boost to string theory. Since supersymmetry is a required component of string theory, any discovered supersymmetry would be consistent with string theory. If the Large Hadron Collider and other major particle physics experiments fail to detect supersymmetric partners or evidence of extra dimensions, many versions of string theory which had predicted certain low mass superpartners to existing particles may need to be significantly revised. The failure of experiments to discover either supersymmetric partners or extra spatial dimensions, as of 2013, has encouraged loop quantum gravity researchers.

Current status

Supersymmetric models are constrained by a variety of experiments, including measurements of low-energy observables – for example, the anomalous magnetic moment of the muon at Brookhaven; the WMAP dark matter density measurement and direct detection experiments – for example, XENON-100 and LUX; and by particle collider experiments, including B-physics, Higgs phenomenology and direct searches for superpartners (sparticles), at the Large Electron–Positron Collider, Tevatron and the LHC.

Historically, the tightest limits were from direct production at colliders. The first mass limits for squarks and gluinos were made at CERN by the UA1 experiment and the UA2 experiment at the Super Proton Synchrotron. LEP later set very strong limits.,[27] which in 2006 were extended by the D0 experiment at the Tevatron.[28][29] From 2003, WMAP's and Planck's dark matter density measurements have strongly constrained supersymmetry models, which, if they explain dark matter, have to be tuned to invoke a particular mechanism to sufficiently reduce the neutralino density.

Prior to the beginning of the LHC, in 2009 fits of available data to CMSSM and NUHM1 indicated that squarks and gluinos were most likely to have masses in the 500 to 800 GeV range, though values as high as 2.5 TeV were allowed with low probabilities. Neutralinos and sleptons were expected to be quite light, with the lightest neutralino and the lightest stau most likely to be found between 100 to 150 GeV.[30]

The first run of the LHC found no evidence for supersymmetry, and, as a result, surpassed existing experimental limits from the Large Electron–Positron Collider and Tevatron and partially excluded the aforementioned expected ranges.[31]

During 2011 and 2012, the LHC discovered a Higgs boson with a mass of about 125 GeV, and with couplings to fermions and bosons which are consistent with the Standard Model. The MSSM predicts that the mass of the lightest Higgs boson should not be much higher than the mass of the Z boson, and, in the absence of fine tuning (with the supersymmetry breaking scale on the order of 1 TeV), should not exceed 130 GeV. Furthermore, for values of the MSSM parameter tan β ≤ 3, it predicts a Higgs mass below 114 GeV over most of the parameter space.[32] This region of Higgs mass was excluded by LEP by 2000. The LHC result is somewhat problematic for the minimal supersymmetric model, as the value of 125 GeV is relatively large for the model and can only be achieved with large radiative loop corrections from top squarks, which many theorists consider to be "unnatural" (see naturalness and fine tuning).[33] On the other hand, the lightest Higgs boson in the MSSM is Standard Model-like, which is consistent with measurements of the Higgs boson couplings at the LHC.

In spite of the null searches and the heavy Higgs, a recent analysis of the constrained minimal supersymmetric Standard Model, the CMSSM, suggests that the model is still compatible with all present experimental constraints.[34][35] The preferred masses for squarks and gluinos is about 2 TeV. The resulting fine-tuning of the electroweak scale, however, is considered "unnatural" (see little hierarchy problem), and some theorists now favor extended supersymmetry models – for example, the NMSSM.

See also

References

  1. ↑ Haber, Howie. "SUPERSYMMETRY, PART I (THEORY)" (PDF). Reviews, Tables and Plots. Particle Data Group (PDG). Retrieved 8 July 2015.
  2. ↑ Martin, Stephen P. (1997). "A Supersymmetry Primer". arXiv:hep-ph/9709356.
  3. ↑ Dine, Michael (2007). Supersymmetry and String Theory: Beyond the Standard Model. p. 169.
  4. ↑ Ellis, John. "The Physics Landscape after the Higgs Discovery at the LHC". arXiv. Invited plenary talk at SILAFAE 2014. Retrieved 8 July 2015.
  5. ↑ Wolchover, Natalie (November 20, 2012). "Supersymmetry Fails Test, Forcing Physics to Seek New Ideas". Quanta Magazine.
  6. ↑ Jonathan Feng: Supersymmetric Dark Matter (pdf), University of California, Irvine, 11 May 2007
  7. ↑ Torsten Bringmann: The WIMP "Miracle" (pdf) University of Hamburg
  8. ↑ R. Haag, J. T. Lopuszanski and M. Sohnius, "All Possible Generators Of Supersymmetries Of The S Matrix", Nucl. Phys. B 88 (1975) 257
  9. ↑ H. Miyazawa (1966). "Baryon Number Changing Currents". Prog. Theor. Phys. 36 (6): 1266–1276. Bibcode:1966PThPh..36.1266M. doi:10.1143/PTP.36.1266.
  10. ↑ H. Miyazawa (1968). "Spinor Currents and Symmetries of Baryons and Mesons". Phys. Rev. 170 (5): 1586–1590. Bibcode:1968PhRv..170.1586M. doi:10.1103/PhysRev.170.1586.
  11. ↑ Michio Kaku, Quantum Field Theory, ISBN 0-19-509158-2, pg 663.
  12. ↑ Peter Freund, Introduction to Supersymmetry, ISBN 0-521-35675-X, pages 26-27, 138.
  13. ↑ Gervais, J. -L.; Sakita, B. (1971). "Field theory interpretation of supergauges in dual models". Nuclear Physics B 34 (2): 632–639. Bibcode:1971NuPhB..34..632G. doi:10.1016/0550-3213(71)90351-8.
  14. ↑ D.V. Volkov, V.P. Akulov, Pisma Zh.Eksp.Teor.Fiz. 16 (1972) 621; Phys.Lett. B46 (1973) 109; V.P. Akulov, D.V. Volkov, Teor.Mat.Fiz. 18 (1974) 39
  15. ↑ Ramond, P. (1971). "Dual Theory for Free Fermions". Physical Review D 3 (10): 2415–2418. Bibcode:1971PhRvD...3.2415R. doi:10.1103/PhysRevD.3.2415.
  16. ↑ Wess, J.; Zumino, B. (1974). "Supergauge transformations in four dimensions". Nuclear Physics B 70: 39–50. Bibcode:1974NuPhB..70...39W. doi:10.1016/0550-3213(74)90355-1.
  17. ↑ http://users.physik.fu-berlin.de/~kleinert/kleinert/?p=supersym suggested here
  18. ↑ Iachello, F. (1980). "Dynamical Supersymmetries in Nuclei". Physical Review Letters 44 (12): 772–775. Bibcode:1980PhRvL..44..772I. doi:10.1103/PhysRevLett.44.772.
  19. ↑ Friedan, D.; Qiu, Z.; Shenker, S. (1984). "Conformal Invariance, Unitarity, and Critical Exponents in Two Dimensions". Physical Review Letters 52 (18): 1575–1578. Bibcode:1984PhRvL..52.1575F. doi:10.1103/PhysRevLett.52.1575.
  20. 1 2 Gordon L. Kane, The Dawn of Physics Beyond the Standard Model, Scientific American, June 2003, page 60 and The frontiers of physics, special edition, Vol 15, #3, page 8
  21. ↑ Supersymmetry in Disorder and Chaos, Konstantin Efetov, Cambridge university press, 1997.
  22. ↑ Miri, M.-A.; Heinrich, M.; El-Ganainy, R.; Christodoulides, D. N. (2013). "Superymmetric optical structures". Physical Review Letters (APS) 110 (23): 233902. arXiv:1304.6646. Bibcode:2013PhRvL.110w3902M. doi:10.1103/PhysRevLett.110.233902. PMID 25167493. Retrieved April 2014.
  23. ↑ Heinrich, M.; Miri, M.-A.; Stützer, S.; El-Ganainy, R.; Nolte, S.; Szameit, A.; Christodoulides, D. N. (2014). "Superymmetric mode converters". Nature Communications (NPG) 5: 3698. arXiv:1401.5734. Bibcode:2014NatCo...5E3698H. doi:10.1038/ncomms4698. PMID 24739256. Retrieved April 2014.
  24. ↑ Miri, M.-A.; Heinrich, Matthias; Christodoulides, D. N. (2014). "SUSY-inspired one-dimensional transformation optics". Optica (OSA) 1 (2): 89. arXiv:1408.0832. doi:10.1364/OPTICA.1.000089. Retrieved August 2014.
  25. ↑ Krasnitz, Michael (2002). Correlation functions in supersymmetric gauge theories from supergravity fluctuafluctuations hHKtions (PDF). Princeton University Department of Physics: Princeton University Department of Physics. p. 91.
  26. ↑ Polchinski,J. String theory. Vol. 2: Superstring theory and beyond, Appendix B
  27. ↑ LEPSUSYWG, ALEPH, DELPHI, L3 and OPAL experiments, charginos, large m0 LEPSUSYWG/01-03.1
  28. ↑ The D0-Collaboration (2009). "Search for associated production of charginos and neutralinos in the trilepton final state using 2.3 fb−1 of data". arXiv:0901.0646. Bibcode:2009PhLB..680...34D. doi:10.1016/j.physletb.2009.08.011.
  29. ↑ The D0 Collaboration (2006). "Search for squarks and gluinos in events with jets and missing transverse energy using 2.1 fb-1 of pp¯ collision data at s=1.96 TeV". arXiv:0712.3805. Bibcode:2008PhLB..660..449D. doi:10.1016/j.physletb.2008.01.042.
  30. ↑ O. Buchmueller; et al. (2009). "Likelihood Functions for Supersymmetric Observables in Frequentist Analyses of the CMSSM and NUHM1". The European Physical Journal C 64 (3): 391–415. arXiv:0907.5568. Bibcode:2009EPJC...64..391B. doi:10.1140/epjc/s10052-009-1159-z.
  31. ↑ Roszkowski, Leszek; Sessolo, Enrico Maria; Williams, Andrew J. (11 August 2014). "What next for the CMSSM and the NUHM: improved prospects for superpartner and dark matter detection". Journal of High Energy Physics 2014 (8). doi:10.1007/JHEP08(2014)067.
  32. ↑ Marcela Carena and Howard E. Haber; Haber (1970). "Higgs Boson Theory and Phenomenology". Progress in Particle and Nuclear Physics 50: 63–152. arXiv:hep-ph/0208209v3. Bibcode:2003PrPNP..50...63C. doi:10.1016/S0146-6410(02)00177-1.
  33. ↑ Patrick Draper; et al. (December 2011). "Implications of a 125 GeV Higgs for the MSSM and Low-Scale SUSY Breaking". Physical Review D 85 (9): 095007. arXiv:1112.3068. Bibcode:2012PhRvD..85i5007D. doi:10.1103/PhysRevD.85.095007.
  34. ↑ Bechtle, Philip. "How alive is constrained SUSY really?". arXiv. Retrieved 8 July 2015.
  35. ↑ Jan de Vries, Kees. "SUSY fits with full LHC Run I data". arXiv. Retrieved 8 July 2015.

Further reading

Theoretical introductions, free and online

Monographs

  • Weak Scale Supersymmetry by Howard Baer and Xerxes Tata, 2006.
  • Cooper, F.; Khare, A.; Sukhatme, U. (1995). "Supersymmetry and quantum mechanics". Physics Reports 251 (5–6): 267–385. doi:10.1016/0370-1573(94)00080-M.  (arXiv:hep-th/9405029).
  • Junker, G. (1996). "Supersymmetric Methods in Quantum and Statistical Physics". doi:10.1007/978-3-642-61194-0. ISBN 978-3-540-61591-0. .
  • Gordon L. Kane.Supersymmetry: Unveiling the Ultimate Laws of Nature Basic Books, New York (2001). ISBN 0-7382-0489-7.
  • Gordon L. Kane and Shifman, M., eds. The Supersymmetric World: The Beginnings of the Theory, World Scientific, Singapore (2000). ISBN 981-02-4522-X.
  • Weinberg, Steven, The Quantum Theory of Fields, Volume 3: Supersymmetry, Cambridge University Press, Cambridge, (1999). ISBN 0-521-66000-9.
  • Wess, Julius, and Jonathan Bagger, Supersymmetry and Supergravity, Princeton University Press, Princeton, (1992). ISBN 0-691-02530-4.
  • "Concise Encyclopedia of Supersymmetry". 2003. doi:10.1007/1-4020-4522-0. ISBN 978-1-4020-1338-6. 

On experiments

External links

This article is issued from Wikipedia - version of the Friday, February 05, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.