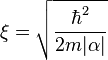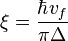Superconducting coherence length

In superconductivity, the superconducting coherence length, usually denoted as \xi (Greek lowercase xi), is the characteristic exponent of the variations of the density of superconducting component.

In some special limiting cases, for example in the weak-coupling BCS theory it is related to characteristic Cooper pair size.

The superconducting coherence length is one of two parameters in the Ginzburg-Landau theory of superconductivity. It is given by:[1]

\xi = \sqrt{\frac{\hbar^2}{2 m |\alpha|}}

while in BCS theory:[2]

\xi = \frac{\hbar v_f}{\pi \Delta}

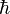where \hbar is the reduced Planck constant, m is the mass of a Cooper pair (twice the electron mass), v_f is the Fermi velocity, and \Delta is the superconducting energy gap.

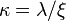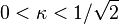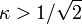The ratio \kappa = \lambda/\xi , where \lambda is the London penetration depth, is known as the Ginzburg–Landau parameter. Type-I superconductors are those with 0<\kappa<1/\sqrt{2}, and type-II superconductors are those with \kappa>1/\sqrt{2}.

For temperatures T near the superconducting critical temperature Tc , ξ(T) ∝ (1-T/Tc)−1.

See also

References

  1. ↑ Tinkham, M. (1996). Introduction to Superconductivity, Second Edition. New York, NY: McGraw-Hill. ISBN 0486435032.
  2. ↑ Annett, James (2004). Superconductivity, Superfluids and Condensates. New York: Oxford university press. p. 62. ISBN 978-0-19-850756-7.
This article is issued from Wikipedia - version of the Monday, December 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.