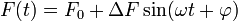Super Bloch oscillations
In physics, a Super Bloch oscillation describes a certain type of motion of a particle in a lattice potential under external periodic driving. The term super refers to the fact that the amplitude in position space of such an oscillation is several orders of magnitude larger than for 'normal' Bloch oscillations.
Bloch oscillations vs. Super Bloch oscillations
Normal Bloch oscillations and Super Bloch oscillations are closely connected. In general, Bloch oscillations are a consequence of the periodic structure of the lattice potential and the existence of a maximum value of the Bloch wave vector 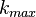 . A constant force
. A constant force  results in the acceleration of the particle until the edge of the first Brillouin zone is reached. The following sudden change in velocity from
results in the acceleration of the particle until the edge of the first Brillouin zone is reached. The following sudden change in velocity from 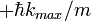 to
to 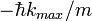 can be interpreted as a Bragg scattering of the particle by the lattice potential. As a result, the velocity of the particle never exceeds
can be interpreted as a Bragg scattering of the particle by the lattice potential. As a result, the velocity of the particle never exceeds 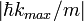 but oscillates in a saw-tooth like manner with a corresponding periodic oscillation in position space. Surprisingly, despite of the constant acceleration the particle does not translate, but just moves over very few lattice sites.
but oscillates in a saw-tooth like manner with a corresponding periodic oscillation in position space. Surprisingly, despite of the constant acceleration the particle does not translate, but just moves over very few lattice sites.
Super Bloch oscillations arise when an additional periodic driving force is added to  , resulting in:
, resulting in:
The details of the motion depend on the ratio between the driving frequency 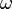 and the Bloch frequency
and the Bloch frequency 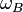 . A small detuning
. A small detuning 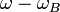 results in a beat between the Bloch cycle and the drive, with a drastic change of the particle motion. On top of the Bloch oscillation, the motion shows a much larger oscillation in position space that extends over hundreds of lattice sites. Those Super Bloch oscillations directly correspond to the motion of normal Bloch oscillations, just rescaled in space and time.
results in a beat between the Bloch cycle and the drive, with a drastic change of the particle motion. On top of the Bloch oscillation, the motion shows a much larger oscillation in position space that extends over hundreds of lattice sites. Those Super Bloch oscillations directly correspond to the motion of normal Bloch oscillations, just rescaled in space and time.
A quantum mechanical description of the rescaling can be found in . An experimental realization is demonstrated in . A theoretical analysis of the properties of Super-Bloch Oscillations, including dependence on the phase of the driving field is found in .
References
- Dynamics of interacting atoms in driven tilted optical lattices. A. Kolovsky and H.J. Korsch, arXiv:0912.2587 (2009)
- Engineering the quantum transport of atomic wavefunctions over macroscopic distances. A. Alberti, V. V. Ivanov, G. M. Tino and G. Ferrari, Nature Phys. 5, 547 (2009)
- Theoretical analysis of quantum dynamics in one-dimensional lattices: Wannier-Stark description. Q. Thommen, J. C. Garreau and V. Zehnle, Phys. Rev. A 65, 053406 (2002)
- Inducing Transport in a Dissipation-Free Lattice with Super Bloch Oscillations. E. Haller, R. Hart, M. J. Mark, J. G. Danzl, L. Reichsöllner and H.-C. Nägerl,Phys. Rev. Lett. 104, 200403 (2010)
- Theoretical Analysis of Super-Bloch Oscillations. K.Kudo and T S Monteiro, Phys.Rev.A. 83, 053627 (2011).