Sunflower (mathematics)

In mathematics, a sunflower or 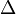 -system is a collection of sets whose pairwise intersection is constant, and called the kernel.
-system is a collection of sets whose pairwise intersection is constant, and called the kernel.
The 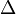 -lemma, sunflower lemma, and sunflower conjecture give various conditions that imply the existence of a large sunflower in a given collection of sets.
-lemma, sunflower lemma, and sunflower conjecture give various conditions that imply the existence of a large sunflower in a given collection of sets.
The original term for this concept was "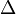 -system". More recently the term "sunflower", possibly introduced by Deza & Frankl (1981), has been gradually replacing it.
-system". More recently the term "sunflower", possibly introduced by Deza & Frankl (1981), has been gradually replacing it.
Formal definition
Suppose 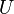 is a universe set and
is a universe set and 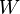 is a collection of subsets of
is a collection of subsets of 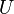 . The collection
. The collection 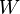 is a sunflower (or
is a sunflower (or 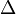 -system) if there is a subset
-system) if there is a subset  of
of 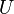 such that for each distinct
such that for each distinct  and
and  in
in 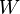 , we have
, we have 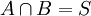 . In other words,
. In other words, 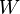 is a sunflower if the pairwise intersection of each set in
is a sunflower if the pairwise intersection of each set in 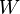 is constant.
is constant.
Δ-lemma
The 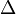 -lemma states that every uncountable collection of finite sets contains an uncountable
-lemma states that every uncountable collection of finite sets contains an uncountable 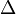 -system.
-system.
The 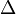 -lemma is a combinatorial set-theoretic tool used in proofs to impose an upper bound on the size of a collection of pairwise incompatible elements in a forcing poset. It may for example be used as one of the ingredients in a proof showing that it is consistent with Zermelo-Fraenkel set theory that the continuum hypothesis does not hold. It was introduced by Shanin (1946).
-lemma is a combinatorial set-theoretic tool used in proofs to impose an upper bound on the size of a collection of pairwise incompatible elements in a forcing poset. It may for example be used as one of the ingredients in a proof showing that it is consistent with Zermelo-Fraenkel set theory that the continuum hypothesis does not hold. It was introduced by Shanin (1946).
Δ-lemma for ω2
If 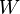 is an
is an 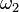 -sized collection of countable subsets of
-sized collection of countable subsets of 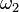 , and if the continuum hypothesis holds, then there is an
, and if the continuum hypothesis holds, then there is an 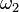 -sized
-sized 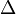 -subsystem. Let
-subsystem. Let 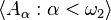 enumerate
enumerate 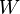 . For
. For 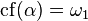 , let
, let
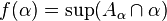 . By Fodor's lemma, fix
. By Fodor's lemma, fix  stationary in
stationary in 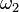 such that
such that  is constantly equal to
is constantly equal to 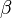 on
on  .
Build
.
Build 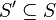 of cardinality
of cardinality 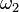 such that whenever
such that whenever  are in
are in 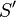 then
then 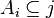 . Using the continuum hypothesis, there are only
. Using the continuum hypothesis, there are only  -many countable subsets of
-many countable subsets of 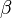 , so by further thinning we may stabilize the kernel.
, so by further thinning we may stabilize the kernel.
Sunflower lemma and conjecture
Erdős & Rado (1960, p. 86) proved the sunflower lemma, stating that if  and
and  are positive integers then a collection of
are positive integers then a collection of 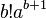 sets of cardinality at most
sets of cardinality at most  contains a sunflower with more than a sets. The sunflower conjecture is one of several variations of the conjecture of (Erdős & Rado 1960, p. 86) that the factor of
contains a sunflower with more than a sets. The sunflower conjecture is one of several variations of the conjecture of (Erdős & Rado 1960, p. 86) that the factor of 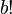 can be replaced by
can be replaced by 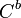 for some constant
for some constant 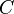 .
.
References
- Deza, M.; Frankl, P. (1981), "Every large set of equidistant (0,+1,–1)-vectors forms a sunflower", Combinatorica 1 (3): 225–231, doi:10.1007/BF02579328, ISSN 0209-9683, MR 637827
- Erdős, Paul; Rado, R. (1960), "Intersection theorems for systems of sets", Journal of the London Mathematical Society, Second Series 35 (1): 85–90, doi:10.1112/jlms/s1-35.1.85, ISSN 0024-6107, MR 0111692
- Jech, Thomas (2003). Set Theory. Springer.
- Kunen, Kenneth (1980). Set Theory: An Introduction to Independence Proofs. North-Holland. ISBN 0-444-85401-0.
- Shanin, N. A. (1946), "A theorem from the general theory of sets", C. R. (Doklady) Acad. Sci. URSS (N.S.) 53: 399–400