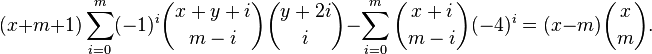Sun's curious identity

In combinatorics, Sun's curious identity is the following identity involving binomial coefficients, first established by Zhi-Wei Sun in 2002:

(x+m+1)\sum_{i=0}^m(-1)^i\dbinom{x+y+i}{m-i}\dbinom{y+2i}{i} -\sum_{i=0}^{m}\dbinom{x+i}{m-i}(-4)^i=(x-m)\dbinom{x}{m}.

After Sun's publication of this identity, five other proofs were obtained by various mathematicians: they are Panholzer and Prodinger's proof via generating functions, Merlini and Sprugnoli's proof using Riordan arrays, Ekhad and Mohammed's proof by the WZ method, Chu and Claudio's proof with the help of Jensen's formula, and Callan's combinatorial proof involving dominos and colorings.

References

Callan, D. (2004), "A combinatorial proof of Sun's 'curious' identity" (PDF), Integers: Electronic Journal of Combinatorial Number Theory 4: A05, arXiv:math.CO/0401216 .

Chu, W.; Claudio, L.V.D. (2003), "Jensen proof of a curious binomial identity" (PDF), Integers: Electronic Journal of Combinatorial Number Theory 3: A20 .

Ekhad, S. B.; Mohammed, M. (2003), "A WZ proof of a 'curious' identity" (PDF), Integers: Electronic Journal of Combinatorial Number Theory 3: A06 .

Merlini, D.; Sprugnoli, R. (2002), "A Riordan array proof of a curious identity" (PDF), Integers: Electronic Journal of Combinatorial Number Theory 2: A08 .

Panholzer, A.; Prodinger, H. (2002), "A generating functions proof of a curious identity" (PDF), Integers: Electronic Journal of Combinatorial Number Theory 2: A06 .

Sun, Zhi-Wei (2002), "A curious identity involving binomial coefficients" (PDF), Integers: Electronic Journal of Combinatorial Number Theory 2: A04 .

Sun, Zhi-Wei (2008), "On sums of binomial coefficients and their applications", Discrete Mathematics 308 (18): 4231–4245, arXiv:math.NT/0404385, doi:10.1016/j.disc.2007.08.046 .

This article is issued from Wikipedia - version of the Friday, November 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.