Sum of radicals
In computational complexity theory there is an open problem whether some information about the sum of radicals may be computed in polynomial time depending on the input size, i.e., in the number of bits necessary to represent this sum. It is of importance for many problems in computational geometry, since the computation of the Euclidean distance between two points in general case involves the computation of a square root, and therefore the perimeter of a polygon or the length of a polygonal chain takes the form of a sum of radicals.[1]
The sum of radicals is defined as a finite linear combination of radicals:
where 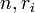 are natural numbers and
are natural numbers and 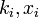 are real numbers.
are real numbers.
Most theoretical research in computational geometry of combinatorial character assumes the computational model of infinite precision real RAM, i.e., an abstract computer in which real numbers and operations with them are performed with infinite precision and the input size of a real number and the cost of an elementary operation are constants.[2] However there is research in computational complexity, especially in computer algebra, where the input size of a number is the number of bits necessary for its representation.[3]
In particular, of interest in computational geometry is the problem of determining the sign of the sum of radicals. For instance, the length of a polygonal path in which all vertices have integer coordinates may be expressed using the Pythagorean theorem as a sum of integer square roots, so in order to determine whether one path is longer or shorter than another in a Euclidean shortest path problem, it is necessary to determine the sign of an expression in which the first path's length is subtracted from the second; this expression is a sum of radicals.
In a similar way, the sum of radicals problem is inherent in the problem of minimum-weight triangulation in the Euclidean metric.
In 1991, Blömer proposed a polynomial time Monte Carlo algorithm for determining whether a sum of radicals is zero, or more generally whether it represents a rational number.[4] While Blömer's result does not resolve the computational complexity of finding the sign of the sum of radicals, it does imply that if the latter problem is in class NP, then it is also in co-NP.[4]
See also
References
- ↑ Wolfgang Mulzer, Günter Rote, "Minimum-Weight Triangulation Is NP-Hard", In: Proceedings of the 22nd Annual Symposium on Computational Geometry, Sedona, June 5–7, 2006, Journal of the ACM, Vol. 55, No. 2, 2008.
- ↑ Franco P. Preparata and Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. ISBN 0-387-96131-3. 1st edition: 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3; Russian translation, 1989: ISBN 5-03-001041-6.
- ↑ Computer Algebra Handbook, 2003, ISBN 3-540-65466-6
- 1 2 Blömer, Johannes (1991). "Computing sums of radicals in polynomial time": 670. doi:10.1109/SFCS.1991.185434..
![\Sigma_{i=1}^n k_i \sqrt[r_i]{x_i},](../I/m/33a31c752d4adf9cd02c86506abe6443.png)