Sugeno integral

In mathematics, the Sugeno integral, named after M. Sugeno,^[1] is a type of integral with respect to a fuzzy measure.

Let 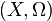$(X,\Omega)$ be a measurable space and let $h:X\to[0,1]$ be an $\Omega$ -measurable function.

The Sugeno integral over the crisp set 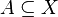$A \subseteq X$ of the function $h$ with respect to the fuzzy measure $g$ is defined by:

\int_A h(x) \circ g = {\sup_{E\subseteq X}} \left[\min\left(\min_{x\in E} h(x), g(A\cap E)\right)\right] = {\sup_{\alpha\in [0,1]}} \left[\min\left(\alpha, g(A\cap F_\alpha)\right)\right]

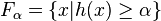where $F_\alpha = \left\{x | h(x) \geq \alpha \right\}$ .

The Sugeno integral over the fuzzy set 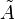$\tilde{A}$ of the function $h$ with respect to the fuzzy measure $g$ is defined by:

\int_A h(x) \circ g = \int_X \left[h_A(x) \wedge h(x)\right] \circ g

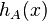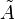where $h_A(x)$ is the membership function of the fuzzy set $\tilde{A}$ .

References

Gunther Schmidt Relational Mathematics, Encyclopedia of Mathematics and its Applications, vol. 132, Cambridge University Press, 2011, ISBN 978-0-521-76268-7
Gunther Schmidt Relational Measures and Integration. pp. 343{357 in Schmidt, R. A., Ed. RelMiCS '9 | Relations and Kleene-Algebra in Computer Science (2006), no. 4136 in Lect. Notes in Comput. Sci., Springer-Verlag

↑ Sugeno, M., Theory of fuzzy integrals and its applieations, Doctoral. Thesis, Tokyo Institute of Technology, 1974

This article is issued from Wikipedia - version of the Sunday, January 04, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.