Strange–Rahman–Smith equation

The Strange–Rahman–Smith equation is used in the cryoporometry method of measuring porosity. NMR cryoporometry ^[1]^[2]^[3] is a recent technique for measuring total porosity and pore size distributions. NMRC is based on two equations, the Gibbs–Thomson equation, that maps the melting point depression to pore size, and the Strange–Rahman–Smith equation ^[1] that maps the melted signal amplitude at a particular temperature to pore volume.

Equation

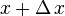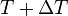If the pores of the porous material are filled with a liquid, then the incremental volume of the pores $\Delta v$ with pore diameter between $x$ and $x + \Delta\,x$ may be obtained from the increase in melted liquid volume for an increase of temperature between $T$ and $T + \Delta T$ by:^[1]

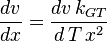
$\frac{dv}{dx} = \frac{dv\,k_{GT}}{d\,T\,x^2}$

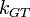Where: $k_{GT}$ is the Gibbs–Thomson coefficient for the liquid in the pores.

References

1 2 3 Strange, J.H.; Rahman, M.; Smith, E.G. (Nov 1993), "Characterization of Porous Solids by NMR", Phys. Rev. Lett. 71 (21): 3589–3591, Bibcode:1993PhRvL..71.3589S, doi:10.1103/PhysRevLett.71.3589, PMID 10055015
↑ Mitchell, J.; Webber, J. Beau W.; Strange, J.H. (2008), "Nuclear Magnetic Resonance Cryoporometry", Phys. Rep. (Review) 461: 1–36, Bibcode:2008PhR...461....1M, doi:10.1016/j.physrep.2008.02.001
↑ SE-10044 Stockholm Sweden. [Furo Istvan Royal Inst TechnolDiv Phys Chem Dept Chem SE-10044 Stockholm Sweden. Royal Inst Chem SE-10044 Stockholm Sweden. [Furo Istvan] Royal Inst Technol Technol Ind NMR Ctr Dept Chem SE-10044 Stockholm Sweden. Div Phys Chem Dept Chem SE-10044 Stockholm Sweden. Royal Inst], "NMR cryoporometry: Principles applications and potential"

This article is issued from Wikipedia - version of the Sunday, April 13, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.