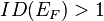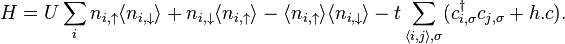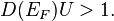Stoner criterion

The Stoner criterion is a condition to be fulfilled for the ferromagnetic order to arise in a simplified model of a solid. It is named after Edmund Clifton Stoner.

Stoner model of ferromagnetism

Ferromagnetism ultimately stems from electron-electron interactions. The simplified model of a solid which is nowadays usually called the Stoner model, can be formulated in terms of dispersion relations for spin up and spin down electrons,

E_\uparrow(k)=\epsilon(k)-I\frac{N_\uparrow-N_\downarrow}{N},\qquad E_\downarrow(k)=\epsilon(k)+I\frac{N_\uparrow-N_\downarrow}{N},

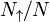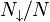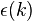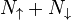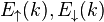where the second term accounts for the exchange energy, $N_\uparrow/N$ ( $N_\downarrow/N$ ) is the dimensionless density[1] of spin up (down) electrons and $\epsilon(k)$ is the dispersion relation of spinless electrons where the electron-electron interaction is disregarded. 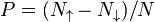If $N_\uparrow +N_\downarrow$ is fixed, $E_\uparrow(k), E_\downarrow(k)$ can be used to calculate the total energy of the system as a function of its polarization $P=(N_\uparrow-N_\downarrow)/N$ . If the lowest total energy is found for P=0, the system prefers to remain paramagnetic but for larger values of I, polarized ground states occur. It can be shown that for

ID(E_F) > 1

the P=0 state will spontaneously pass into a polarized one. This is the Stoner criterion, expressed in terms of the P=0 density of states[1] at the Fermi level 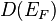$D(E_F)$ .

Note that a non-zero P state may be favoured over P=0 even before the Stoner criterion is fulfilled.

Relationship to the Hubbard model

The Stoner model can be obtained from the Hubbard model by applying the mean-field approximation. The particle density operators are written as their mean value 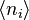$\langle n_i\rangle$ plus fluctuation 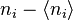$n_i-\langle n_i\rangle$ and the product of spin-up and spin-down fluctuations is neglected. We obtain[1]

H = U \sum_i n_{i,\uparrow} \langle n_{i,\downarrow}\rangle +n_{i,\downarrow} \langle n_{i,\uparrow}\rangle - \langle n_{i,\uparrow}\rangle \langle n_{i,\downarrow}\rangle - t \sum_{\langle i,j\rangle,\sigma} (c^{\dagger}_{i,\sigma}c_{j,\sigma}+h.c).

Note the third term which was omitted in the definition above. With this term included, we arrive at the better-known form of the Stoner criterion

D(E_F)U > 1.

References

Stephen Blundell, Magnetism in Condensed Matter (Oxford Master Series in Physics).
Teodorescu, C. M.; Lungu, G. A. (November 2008). "Band ferromagnetism in systems of variable dimensionality". Journal of Optoelectronics and Advanced Materials 10 (11): 3058–3068. Retrieved 24 May 2014.

Footnotes

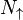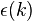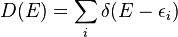1. Having a lattice model in mind, N is the number of lattice sites and $N_\uparrow$ is the number of spin-up electrons in the whole system. The density of states has the units of inverse energy. On a finite lattice, $\epsilon(k)$ is replaced by discrete levels $\epsilon_i$ and then $D(E)=\sum_i \delta(E-\epsilon_i)$ .

This article is issued from Wikipedia - version of the Wednesday, February 10, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.