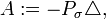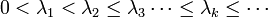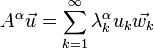Stokes operator
The Stokes operator, named after George Gabriel Stokes, is an unbounded linear operator used in the theory of partial differential equations, specifically in the fields of fluid dynamics and electromagnetics.
Definition
If we define 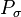 as the Leray projection onto divergence free vector fields, then the Stokes Operator
as the Leray projection onto divergence free vector fields, then the Stokes Operator  is defined by
is defined by
where 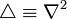 is the Laplacian. Since
is the Laplacian. Since  is unbounded, we must also give its domain of definition, which is defined as
is unbounded, we must also give its domain of definition, which is defined as 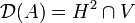 , where
, where 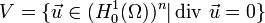 . Here,
. Here,  is a bounded open set in
is a bounded open set in 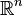 (usually n = 2 or 3),
(usually n = 2 or 3),  and
and  are the standard Sobolev spaces, and the divergence of
are the standard Sobolev spaces, and the divergence of 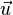 is taken in the distribution sense.
is taken in the distribution sense.
Properties
For a given domain  which is open, bounded, and has
which is open, bounded, and has  boundary, the Stokes operator
boundary, the Stokes operator  is a self-adjoint positive-definite operator with respect to the
is a self-adjoint positive-definite operator with respect to the 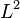 inner product. It has an orthonormal basis of eigenfunctions
inner product. It has an orthonormal basis of eigenfunctions 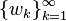 corresponding to eigenvalues
corresponding to eigenvalues 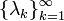 which satisfy
which satisfy
and  as
as  . Note that the smallest eigenvalue is unique and non-zero. These properties allow one to define powers of the Stokes operator. Let
. Note that the smallest eigenvalue is unique and non-zero. These properties allow one to define powers of the Stokes operator. Let  be a real number. We define
be a real number. We define  by its action on
by its action on 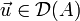 :
:
where 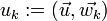 and
and  is the
is the  inner product.
inner product.
The inverse  of the Stokes operator is a bounded, compact, self-adjoint operator in the space
of the Stokes operator is a bounded, compact, self-adjoint operator in the space 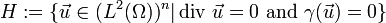 , where
, where  is the trace operator. Furthermore,
is the trace operator. Furthermore, 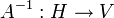 is injective.
is injective.
References
- Temam, Roger (2001), Navier-Stokes Equations: Theory and Numerical Analysis, AMS Chelsea Publishing, ISBN 0-8218-2737-5
- Constantin, Peter and Foias, Ciprian. Navier-Stokes Equations, University of Chicago Press, (1988)