Stochastic cellular automaton
Stochastic cellular automata or 'probabilistic cellular automata' (PCA) or 'random cellular automata' or locally interacting Markov chains[1][2] are an important extension of cellular automaton. Cellular automata are a discrete-time dynamical system of interacting entities, whose state is discrete.
The state of the collection of entities is updated at each discrete time according to some simple homogeneous rule. All entities' states are updated in parallel or synchronously. Stochastic Cellular Automata are CA whose updating rule is a stochastic one, which means the new entities' states are chosen according to some probability distributions. It is a discrete-time random dynamical system. From the spatial interaction between the entities, despite the simplicity of the updating rules, complex behaviour may emerge like self-organization. As mathematical object, it may be considered in the framework of stochastic processes as an interacting particle system in discrete-time.
PCA as Markov stochastic processes
As discrete-time Markov process, PCA are defined on a product space 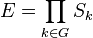 (cartesian product) where
(cartesian product) where  is a finite or infinite graph, like
is a finite or infinite graph, like  and where
and where  is a finite space, like for instance
is a finite space, like for instance
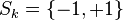 or
or 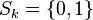 . The transition probability has a product form
. The transition probability has a product form
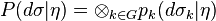 where
where
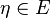 and
and 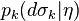 is a probability distribution on
is a probability distribution on  .
In general some locality is required
.
In general some locality is required 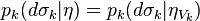 where
where
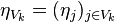 with
with 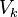 a finite neighbourhood of k. See [3] for a more detailed introduction following the probability theory's point of view.
a finite neighbourhood of k. See [3] for a more detailed introduction following the probability theory's point of view.
Examples of stochastic cellular automaton
Majority cellular automaton
There is a version of the majority cellular automaton with probabilistic updating rules. See the Toom's rule.
Relation to random fields
PCA may be used to simulate the Ising model of ferromagnetism in statistical mechanics.[4] Some categories of models were studied from a statistical mechanics point of view.
Cellular Potts model
There is a strong connection between probabilistic cellular automata and the cellular Potts model in particular when it is implemented in parallel.
References
- ↑ Toom, A. L. (1978), Locally Interacting Systems and their Application in Biology: Proceedings of the School-Seminar on Markov Interaction Processes in Biology, held in Pushchino, March 1976, Lecture Notes in Mathematics 653, Springer-Verlag, Berlin-New York, ISBN 3-540-08450-9, MR 0479791
- ↑ R. L. Dobrushin, V. I. Kri︠u︡kov, A. L. Toom (1978). Stochastic Cellular Systems: Ergodicity, Memory, Morphogenesis. ISBN 9780719022067.
- ↑ P.-Y. Louis PhD
- ↑ Vichniac, G. (1984), "Simulating physics with cellular automata", Physica D 10: 96–115, Bibcode:1984PhyD...10...96V, doi:10.1016/0167-2789(84)90253-7.
Additional reading
- Almeida, R. M.; Macau, E. E. N. (2010), "Stochastic cellular automata model for wildland fire spread dynamics", 9th Brazilian Conference on Dynamics, Control and their Applications, June 7–11, 2010.
- Clarke, K. C.; Hoppen, S. (1997), "A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area" (PDF), Environment and Planning B: Planning and Design 24: 247–261, doi:10.1068/b240247.
- Mahajan, Meena Bhaskar (1992), Studies in language classes defined by different types of time-varying cellular automata, Ph.D. dissertion, Indian Institute of Technology Madras.
- Nishio, Hidenosuke; Kobuchi, Youichi (1975), "Fault tolerant cellular spaces", Journal of Computer and System Sciences 11 (2): 150–170, doi:10.1016/s0022-0000(75)80065-1, MR 0389442.
- Smith, Alvy Ray, III (1972), "Real-time language recognition by one-dimensional cellular automata", Journal of Computer and System Sciences 6: 233–253, doi:10.1016/S0022-0000(72)80004-7, MR 0309383.