Stellated truncated hexahedron
| Stellated truncated hexahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 14, E = 36 V = 24 (χ = 2) |
| Faces by sides | 8{3}+6{8/3} |
| Wythoff symbol | 2 3 | 4/3 2 3/2 | 4/3 |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U19, C66, W92 |
| Dual polyhedron | Great triakis octahedron |
| Vertex figure |  3.8/3.8/3 |
| Bowers acronym | Quith |
In geometry, the stellated truncated hexahedron (or quasitruncated hexahedron) is a uniform star polyhedron, indexed as U19. It is represented by Schläfli symbol t{4/3,3}, and Coxeter-Dynkin diagram, 
. It is sometimes called quasitruncated hexahedron because it is related to the truncated cube, , except that the square faces become inverted into {8/3} octagrams.
Note that stellated truncated hexahedron is not a true stellation of the truncated hexahedron; its convex 'core' is not a uniform polyhedron.
Orthographic projections
Related polyhedra
It shares the vertex arrangement with three other uniform polyhedra: the convex rhombicuboctahedron, the small rhombihexahedron, and the small cubicuboctahedron.
 Rhombicuboctahedron |
 Small cubicuboctahedron |
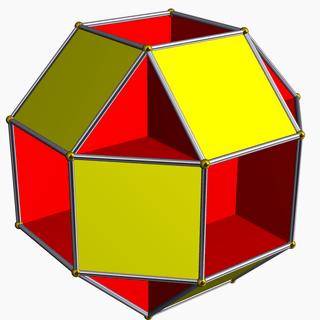 Small rhombihexahedron |
Stellated truncated hexahedron |
See also
External links
This article is issued from Wikipedia - version of the Saturday, January 17, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.